江苏龙网

  1. 首页 > 人文 > >

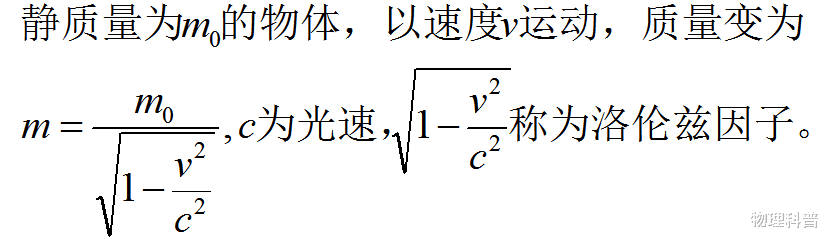
『物理』E=mc^2史上最简明的数学推导，高中基础绝对能看懂！


『物理』E=mc^2史上最简明的数学推导，高中基础绝对能看懂！
文章图片
『物理』E=mc^2史上最简明的数学推导，高中基础绝对能看懂！
文章图片
『物理』E=mc^2史上最简明的数学推导，高中基础绝对能看懂！
网上查了下 ， 发现同类文章全是一些纯粹的积分推导 ， 大多都没有太多的物理内涵 。 因此 ， 决定写一篇质能方程推导的文章 ， 力求以最简明的形式表达出最直接的物理内涵 ， 因为是科普 ， 全文将绝对不会出现积分符号 。
后面推导必须用到微分符号 ， 但这个很简单 ， 这里介绍一下就懂 。 微分符号d就是求一个量的无穷小变化量的意思 。 例如 ， dx就表示变量x的无穷小增量x'-xx'与x无限接近；df(x)表示函数f(x)的值的无穷小增量 ， 它们的比值df(x)/dx就表示对f(x)求导数 ， 导数就是在变量变化时 ， 函数值的变化相比于变量的变化的快慢程度（比值） 。 简单吧！
下面直接给出几个求导的公式 ， 因为下面的推导过程会用到 。
爱因斯坦的狭义相对论建立在狭义相对性原理和光速不变原理的基础上 ， 也就是说物理规律在任何惯性参考系上都应该是相同的 ， 并且光速在任何惯性参考系上都具有相同的数值 。 在此基础之上 ， 爱因斯坦得到了惯性参考系之间的洛伦兹变换 ， 也就是两个惯性参考系之间同一事件的时空坐标的变换关系 。 进一步 ， 爱因斯坦得到了运动物体质量增加的关系式 ， 见下图 。
由牛顿力学可以知道 ， 速度增加 ， 动能就会增加 ， 那么在狭义相对论中 ， 速度的增加引起了质量的增加 ， 这会让我们联想到 ， 增加的动能会以质量的增量的形式蕴含在物体的动质量中 。
【『物理』E=mc^2史上最简明的数学推导，高中基础绝对能看懂！】牛顿力学中 ， 力F与力的作用距离S的乘积代表着能量的传递（做功） ， 例如将一块很重的石头使劲搬到楼顶去 ， 我们搬运石头的向上的力与搬运高度的乘积就会使得石头的势能增加 。 由于力是动量P对时间t的导数 ， 距离S是速度V与时间的乘积T ， 因此约掉时间t ， 能量就是动量P与速度V的乘积 。
因为牛顿的经典力学必须作为狭义相对论在速度远远小于光速时的极限近似 ， 因此牛顿力学中能量的定义必须在狭义相对论中成立 。 这时 ， 我们就可以进行下述推导（如果有不懂的 ， 就看看上文对微分符号及求导的介绍 ， 并注意根号可以写成指数位置为1/2常数的导数为0 ， v的导数为1）：
在上述推导过程中可以看出 ， 动能的增加全部由动量的增加引起 ， 动量的增加则全部由速度的增加引起 。 由于推导的一开始 ， 求的是动能的无穷小增量 ， 这就等价于我们对动质量进行了微分的操作 ， 因此上述推导中的E就是物体以速度v运动时的总能量 ， E=mc^2就表明质量与能量通过光速c等价了起来 。 当速度v取0时 ， 就得到物体的静能量E(0)=m(0)c^2 ， 物体的动能就是mc^2-m(0)c^2 。
如果将物体的能量展开为无穷级数的形式 ， 其中第一项就是m(0)c^2 ， 第二项就是牛顿力学中的动能1/2(m(0)v^2) ， 后面的所有项在速度远远小于光速时 ， 完全就可以省略掉了 。 这也意味着 ， 狭义相对论是牛顿力学的扩展 。
一下午时间 ， 只能简明到这个程度了 ， 如果没看懂 ， 请再仔细看看 ， 就会明白 ， 见谅！精通数学的朋友也可以看出 ， 这个推导方法并不常见 ， 但物理内涵会更加明朗！


    推荐阅读


    上一篇：「高中数学」高中数学：10种求最值的方法，带你玩转，高中生来看

    下一篇：『汉语』俄罗斯“不及格”汉语试卷走红，中国学生无法淡定：一个敢问一个敢答