гҖҺгҖҸдёүи§’еҪўдёӯзҡ„жңҖеҖјй—®йўҳпјҢй«ҳиҖғзғӯзӮ№пјҢ14, 16, 18е№ҙйғҪжңү

ж–Үз« еӣҫзүҮ
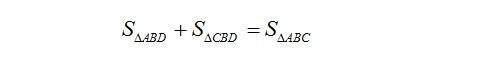
ж–Үз« еӣҫзүҮ

ж–Үз« еӣҫзүҮ

ж–Үз« еӣҫзүҮ

ж–Үз« еӣҫзүҮ

ж–Үз« еӣҫзүҮ
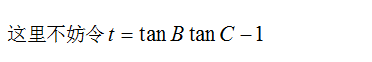
ж–Үз« еӣҫзүҮ
гҖҗгҖҺгҖҸдёүи§’еҪўдёӯзҡ„жңҖеҖјй—®йўҳпјҢй«ҳиҖғзғӯзӮ№пјҢ14, 16, 18е№ҙйғҪжңүгҖ‘
ж–Үз« еӣҫзүҮ

ж–Үз« еӣҫзүҮ

зәөи§ӮиҝҷеҮ е№ҙзҡ„жұҹиӢҸй«ҳиҖғ пјҢ жңүдёҖзұ»йўҳиҖғзҡ„规еҫӢжҖ§еҫҲејә пјҢ 2018гҖҒ2016гҖҒ2014е№ҙйғҪиҖғдәҶ пјҢ 2015гҖҒ2017гҖҒ2019е№ҙжІЎиҖғ пјҢ зңӢзқҖиҝҷе№ҙд»Ҫ пјҢ ж„ҹи§үи·ҹеҒ¶ж•°е№ҙжңүе…і пјҢ 究з«ҹжҳҜд»Җд№ҲйўҳеһӢе‘ўпјҹ
жҲ‘们е…ҲжқҘзңӢдёҖдёӢпјҡ
дёҚйҡҫеҸ‘зҺ° пјҢ иҝҷдёҚе°ұжҳҜдёүи§’еҪўдёӯзҡ„жңҖеҖјй—®йўҳеҗ—пјҹдёҚй”ҷ пјҢ иҖҢдё”жүҖз”ЁеҲ°зҡ„зҹҘиҜҶзӮ№дё»иҰҒжҳҜжӯЈдҪҷејҰе®ҡзҗҶе’Ңеҹәжң¬дёҚзӯүејҸ пјҢ ж„ҹи§үдёҚжҳҜеҫҲйҡҫ пјҢ дҪҶжҳҜд»Һе…¶жүҖеҮәзҺ°зҡ„дҪҚзҪ® пјҢ еҸҲж„ҹи§үдёҚеҘҪжғ№ пјҢ еӣ дёәеЎ«з©әйўҳд№ҹе°ұ14йўҳ пјҢ 13гҖҒ14йўҳеҸҜд»Ҙз®—жҳҜеЎ«з©әйўҳзҡ„еҺӢиҪҙйўҳдәҶ пјҢ и®ёеӨҡеҗҢеӯҰжҜҸж¬ЎеҒҡе®Ң第12йўҳзҡ„ж—¶еҖҷ пјҢ зӣҙжҺҘи·іеҲ°з¬¬15йўҳ пјҢ еҸҜи§ҒжңҖеҗҺдёӨйўҳеңЁеҗҢеӯҰ们еҝғдёӯжүҖеӨ„зҡ„ең°дҪҚ гҖӮ
йӮЈд№Ҳ пјҢ иҝҷзұ»йўҳзңҹзҡ„еҫҲйҡҫеҗ—пјҹжҲ‘们дёҚеҰЁе…ҲзңӢдёҖдёӢиҝҷдёүдёӘйўҳзҡ„и§Јжі•пјҡ
2018е№ҙ13йўҳпјҡе…Ҳз”»еӣҫ пјҢ з ”з©¶дёҖдёӢйҮҢйқўзҡ„ж•°йҮҸе…ізі»пјҡ
дёҚйҡҫеҸ‘зҺ°пјҡ
еҚіпјҡ
еҚіпјҡ
жүҖд»Ҙпјҡ
еңЁжғіжғій—®йўҳй—®зҡ„жҳҜжңүе…іжӯЈеҲҮзҡ„ејҸеӯҗ пјҢ иҰҒд№ҲжҠҠеҲҮеҢ–жҲҗејҰ пјҢ иҰҒд№ҲжҠҠејҰеҢ–жҲҗеҲҮ пјҢ иҝҷдёӘејҰзңӢеҫ—зңјиҠұзјӯд№ұ пјҢ дәҺжҳҜжҲ‘们жҠҠдёҠејҸдёӨиҫ№еҗҢйҷӨд»Ҙ
е°ұеҫ—еҲ°дәҶпјҡ
еӨ§йғЁеҲҶй«ҳдёӯеӯҰз”ҹиҝҳжҳҜиғҪеҒҡеҮәжқҘзҡ„ пјҢ й«ҳдёҖдёҠеӯҰжңҹе°ұеә”иҜҘдјҡдәҶ пјҢ жҳ“зҹҘжңҖе°ҸеҖјдёә8 гҖӮ
2014е№ҙ第14йўҳпјҡжӯӨйўҳдёҖзңӢ пјҢ е°ұжңүејҰеҢ–иҫ№зҡ„еҶІеҠЁпјҡ
з”ұжӯЈејҰе®ҡзҗҶеҫ—пјҡ
д»ҺдёҠиҝ°дёүдёӘйўҳдёҚйҡҫзңӢеҮә пјҢ жүҫзӯүйҮҸе…ізі»гҖҒеҢ–з®ҖзӯүйҮҸе…ізі»йқһеёёйҮҚиҰҒ пјҢ 第дёҖйўҳж №жҚ®зӯүз§Ҝжі•жүҫеҲ°дәҶдёҖдёӘжҜ”иҫғз®ҖжҙҒзҡ„зӯүйҮҸе…ізі» пјҢ 第дәҢйўҳж №жҚ®дёүи§’еҮҪж•°е’Ңе·®еҸҳжҚўе…¬ејҸд»ҘеҸҠеҗҢи§’дёүи§’еҮҪж•°е…ізі»жүҫеҲ°дәҶе·ІзҹҘе’ҢжңӘзҹҘд№Ӣй—ҙзҡ„зәҪеёҰ пјҢ 第дёүйўҳеҲҷжҳҜжӯЈдҪҷејҰе®ҡзҗҶзҡ„е®ҢзҫҺз»“еҗҲ пјҢ еҪ“然иҝҷдёүйўҳжңҖеҗҺдёҖжӯҘйғҪеҪ’еҲ°дәҶеҹәжң¬дёҚзӯүејҸй—ЁдёӢ пјҢ жүҖд»ҘиҰҒи§ЈеҶіжӯӨзұ»й—®йўҳ пјҢ еҗҲзҗҶдҪҝз”ЁжӯЈдҪҷејҰе®ҡзҗҶ пјҢ еҢ–з№Ғдёәз®Җ пјҢ дҪҝеҫ—ж•ҙдҪ“зҡ„и®Ўз®—еҜ№з§°з»ҹдёҖ пјҢ д»ҺиҖҢеҮ»з ҙжӯӨзұ»йўҳ гҖӮ
жҺЁиҚҗйҳ…иҜ»
- дёӯеӨ®иҙўз»ҸеӨ§еӯҰв–ІдёӯеӣҪжңҖеҖјеҫ—дёҠзҡ„6жүҖеӨ§еӯҰ жҜ•дёҡеҗҺе·Ҙиө„й«ҳ, еүҚйҖ”дёҖзүҮе…үжҳҺ
- гҖҺй«ҳиҖғеҝ—ж„ҝгҖҸе…¬еҠЎе‘ҳиҖғиҜ•дёӯжңҖеҸ—ж¬ўиҝҺзҡ„дёӨдёӘдё“дёҡпјҢеҚҙжҳҜй«ҳиҖғеҝ—ж„ҝдёӯзҡ„еҶ·й—Ё
- ж•°еӯҰ@зІү笔дёӯзҡ„вҖңеҠіж–ҜиҺұж–ҜвҖқпјҢж•°еӯҰ家дёәд№Ӣз–ҜзӢӮпјҢзҺ°еңЁиҠұеӨ§д»·й’ұд№ҹеҫҲйҡҫд№°еҲ°
- йҳҝеҹәзұіеҫ·пјҡй«ҳиҖғж•°еӯҰе‘Ҫйўҳзҡ„дёҖдёӘи—Ҹе®қеә“----йҳҝеҹәзұіеҫ·дёүи§’еҪў
- гҖҺй«ҳж ЎгҖҸеӘ’дҪ“еҸЈдёӯзҡ„вҖңд№Ұе‘ҶеӯҗвҖқ: й«ҳиҖғ703еҲҶ, жӢ’з»қжё…еҚҺеҢ—еӨ§, еҗҺиў«11жүҖй«ҳж ЎжӢ’з»қ
- @жҙ»и·ғеңЁй«ҳиҖғиҜ•йўҳдёӯзҡ„йҳҝжіўзҪ—е°јж–ҜеңҶ