зү©зҗҶ|еӣҡзҰҒдәҺзәізұіеӣҙж Ҹдёӯзҡ„йҮҸеӯҗ( е…ӯ )
иҝҷйҮҢзҡ„зү©зҗҶе·Із»Ҹе‘јд№Ӣж¬ІеҮәпјҡзәізұійҮҸеӯҗеӣҙж ҸжӯЈеҘҪеҸҜд»Ҙи°ғжҺ§еӣҙж ҸеҶ…иҙ№зұійқўеӨ„зҡ„з”өеӯҗжҖҒеҜҶеәҰ пјҢ еҜ№еҗ§пјҹпјҒжүҖд»Ҙ пјҢ зәізұійҮҸеӯҗеӣҙж ҸжӯЈеҘҪеҸҜд»Ҙи°ғжҺ§иҝ‘и—Өзі»з»ҹзҡ„иҝ‘и—Өжё©еәҰ пјҢ еҜ№еҗ§пјҹпјҒ
еңЁе®һйӘҢжөӢйҮҸдёҠ пјҢ дҪҺжё©жү«жҸҸйҡ§йҒ“жҳҫеҫ®й•ңеҲҷжҸҗдҫӣдәҶдёҖз§Қз ”з©¶иҝ‘и—Өж•Ҳеә”зҡ„жңүж•ҲжүӢж®ө гҖӮ з”ұдәҺзЈҒжҖ§жқӮиҙЁдёҺдј еҜјз”өеӯҗзҡ„ж•Је°„дә§з”ҹдәҶдёҖз§Қе…ұжҢҜзҺ°иұЎеҚіиҝ‘и—Өе…ұжҢҜ пјҢ иҝ‘и—Өж•Ҳеә”дҪҝеҫ—еңЁзЈҒжҖ§жқӮиҙЁдёҠж–№жөӢеҫ—зҡ„йҡ§йҒ“и°ұеңЁиҙ№зұіиғҪзә§йҷ„иҝ‘е‘ҲзҺ°еҮәе…·жңүдёҖе®ҡе®ҪеәҰзҡ„еі°жҲ–и°· пјҢ е…¶е®ҪеәҰеҸҚжҳ дәҶиҝ‘и—Өжё©еәҰзҡ„й«ҳдҪҺ гҖӮ
е…·дҪ“еҲ°дёҖдёӘжңүйҷҗе°әеҜёдҪ“зі»иҖҢиЁҖ пјҢ е…¶иҙ№зұіжҖҒеҜҶеәҰе°ұжңүдҪ“жҖҒиҙ№зұіжҖҒеҜҶеәҰдёҺиЎЁйқўжҖҒиҙ№зұіжҖҒеҜҶеәҰд№ӢеҲҶ гҖӮ еҲ©з”ЁдҪ“жҖҒеҜҶеәҰжқҘи°ғжҺ§иҝ‘и—Өжё©еәҰзҡ„зү©зҗҶе·Ідј—жүҖе‘ЁзҹҘ пјҢ 然иҖҢиЎЁйқўжҖҒжҳҜеҗҰдёҺиҝ‘и—Өж•Ҳеә”еҜҶеҲҮиҒ”зі» пјҢ жҲ–иҖ…иҜҙиЎЁйқўжҖҒжҳҜеҗҰеҸӮдёҺиҝ‘и—Өж•Ҳеә”и°ғжҺ§еҚҙ并дёҚжҳҺзЎ® гҖӮ иҝҷдёҖй—®йўҳеҺҶеҸІдёҠжӣҫз»ҸжңүиҝҮдёҖж®өж—¶й—ҙзҡ„дәүи®® гҖӮ
зңӢеҗӣйҳ…еҲ°жӯӨеӨ„ пјҢ еә”иҜҘжӣҙеҠ жҳҺдәҶз”ЁйҮҸеӯҗеӣҙж ҸжқҘз ”з©¶иҝ‘и—Өж•Ҳеә”зҡ„д»·еҖјпјҡеӣ дёәеӣҙж ҸеҶ…зҡ„йҮҸеӯҗе°әеҜёж•Ҳеә”е°ұжҳҜй’ҲеҜ№иЎЁйқўжҖҒеҜҶеәҰзҡ„ пјҢ жүҖд»Ҙиҝҷж ·зҡ„з ”з©¶жңүжңӣжҫ„жё…иЎЁйқўжҖҒеҜҶеәҰжҳҜдёҚжҳҜдёҺиҝ‘и—Өж•Ҳеә”жңүеҜҶеҲҮиҒ”зі» пјҢ жҲ–иҖ…иҜҙиЎЁйқўжҖҒеҜҶеәҰиғҪдёҚиғҪеҸӮдёҺи°ғжҺ§иҝ‘и—Өж•Ҳеә” гҖӮ иҝҷж ·зҡ„дёҖдёӘзү©зҗҶзі»з»ҹ пјҢ еҸҜд»Ҙз®—жҳҜиёҸз ҙй“ҒйһӢж— и§…еӨ„ пјҢ дјјд№Һе°ұжҳҜдёәдәҶз ”з©¶иЎЁйқўжҖҒзү©зҗҶиҖҢз”ҹзҡ„ гҖӮ
жҲ‘们й«ҳе…ҙзҡ„жҳҜ пјҢ иҝҷдёҖдәүи®®дёҚд№…еүҚеҫ—еҲ°ж¶Ҳи§Ј пјҢ иҜҰз»Ҷз»“жһңеҸҜеҸӮи§Ғж–ҮзҢ® [Phys. Rev. B 97,035417 (2018)] гҖӮ иҝҷйҮҢ пјҢ жҲ‘们еҸӘз»ҷеҮәз®ҖжҙҒзҡ„жҸҸиҝ°пјҡ
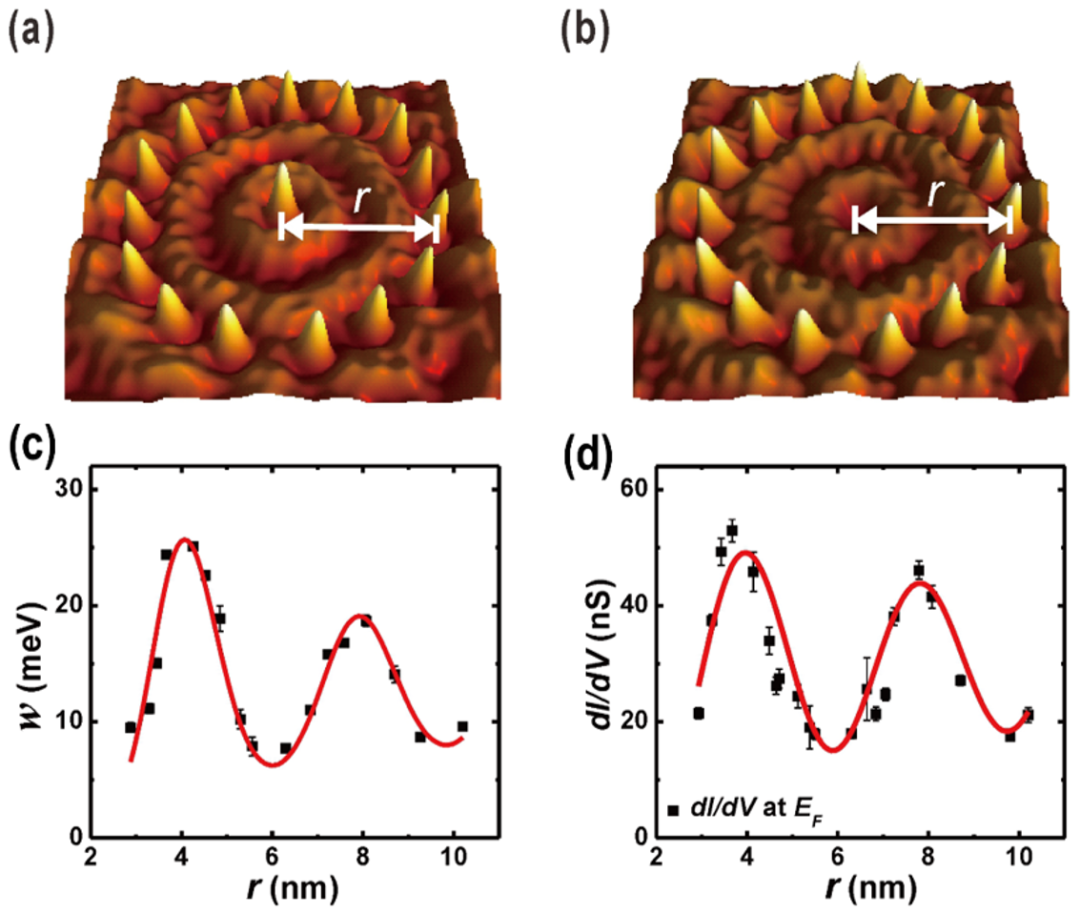
(1) жһ„е»әдёҖдёӘзі»з»ҹпјҡеңЁи¶іеӨҹеӨ§зҡ„ Ag (111) иЎЁйқўжһ„е»әдёҚеҗҢзҡ„ Co еҺҹеӯҗеӣҙж Ҹ пјҢ еҰӮеӣҫ 8(a) е’Ң (b) жүҖзӨә гҖӮ е…¶дёӯ (a) дёӯзҡ„еӣҙж ҸдёӯеҝғжңүдёҖдёӘ Co еҺҹеӯҗ пјҢ (b) дёӯе°ұжІЎжңү гҖӮ иҝҷж ·зҡ„дёӨдёӘзі»з»ҹ пјҢ дёӯеҝғжңүеҺҹеӯҗзҡ„еҚіеҪўжҲҗдёҖдёӘиҝ‘и—ӨдҪ“зі» пјҢ дёӯеҝғз©әзҡ„еӣҙж ҸеҚідёҚжҳҜ гҖӮ
(2) зҺ°еңЁеҜ№ (a) дёӯеӣҙж Ҹдёӯеҝғзҡ„ Co еҺҹеӯҗе®һж–Ҫ STM йҡ§йҒ“и°ұжөӢйҮҸ пјҢ еҫ—еҲ°йҡ§йҒ“и°ұзҡ„иҝ‘и—Өе…ұжҢҜе®ҪеәҰ w (йҮҸзәІдёә meV пјҢ йҷӨд»ҘзҺ»е°”е…№жӣјеёёж•°еҚіеҫ—иҝ‘и—Өжё©еәҰ) гҖӮ й’ҲеҜ№дёҖзі»еҲ—дёҚеҗҢе°әеҜё (еҚҠеҫ„дёә r ) зҡ„еӣҙж Ҹ пјҢ жөӢйҮҸе…¶дёӯеҝғ Co еҺҹеӯҗзҡ„иҝ‘и—Өжё©еәҰ w пјҢ еҫ—еҲ° w дёҺ r зҡ„е…ізі» пјҢ еҰӮеӣҫ 8(c) жүҖзӨә гҖӮ еҸҜд»ҘзңӢеҲ° пјҢ w (r ) е‘ҲзҺ°зҡ„жҳҜдёҖжқЎиЎ°еҮҸжҢҜиҚЎжӣІзәҝ гҖӮ
(3) й’ҲеҜ№еӣҙж ҸдёӯеҝғжІЎжңү Co еҺҹеӯҗзҡ„жғ…еҶө пјҢ еҚідёҚеӯҳеңЁиҝ‘и—Өж•Ҳеә”зҡ„жғ…еҶө пјҢ еҸҜд»ҘжөӢйҮҸиҙ№зұіиғҪзә§еӨ„зҡ„жү«жҸҸйҡ§йҒ“и°ұ пјҢ жҸҗеҸ–е…¶ dI / dV ж•°жҚ® пјҢ д№ҹе°ұжҳҜиЎЁйқўжҖҒеҜҶеәҰзҡ„й«ҳдҪҺ гҖӮ жөӢйҮҸеҸ‘зҺ° пјҢ dI / dV ж•°жҚ®дёҺ r жңүзұ»дјјеҪўзҠ¶зҡ„иЎ°еҮҸжҢҜиҚЎе…ізі» пјҢ еҰӮеӣҫ 8(d) жүҖзӨә гҖӮ
(4) дёӨиҖ…зҡ„зӣёдјјжҖ§жҜ«ж— з–‘д№үең°иҜҒжҳҺиЎЁйқўжҖҒеҜҶеәҰеҜ№иҝ‘и—Өе…ұжҢҜжңүи°ғжҺ§дҪңз”Ё гҖӮ
жң¬ж–ҮеӣҫзүҮ
еӣҫ8. зәізұіеӣҙж ҸеҜ№иҝ‘и—Өе…ұжҢҜе®ҪеәҰ w зҡ„и°ғеҲ¶ гҖӮ еӣҫ (a) е’Ң (b) еҲҶеҲ«дёәдёӯеҝғжңү Co еҺҹеӯҗе’ҢдёӯеҝғжІЎжңү Co еҺҹеӯҗзҡ„ Co еҺҹеӯҗеӣҙж Ҹд№Ӣ STM еҪўиІҢеӣҫ гҖӮ (c) еӣҙж Ҹдёӯеҝғ Co еҺҹеӯҗзҡ„иҝ‘и—Өе…ұжҢҜе®ҪеәҰ w йҡҸеӣҙж ҸеҚҠеҫ„ r зҡ„дҫқиө–е…ізі» гҖӮ (d) дёӯеҝғдёәз©әзҡ„ Co еҺҹеӯҗеӣҙж Ҹзҡ„еұҖеҹҹиЎЁйқўжҖҒеҜҶеәҰ (иҙ№зұіиғҪзә§еӨ„зҡ„жү«жҸҸйҡ§йҒ“и°ұ dI / dV дёҺеӣҙж ҸеҚҠеҫ„ r зҡ„е…ізі» гҖӮ зәўиүІжӣІзәҝжҳҜжӢҹеҗҲз»“жһң гҖӮ еҸӮиҖғж–ҮзҢ® [Phys. Rev. B 97, 035417 (2018)] гҖӮ
6. йҮҸеӯҗйҖ»иҫ‘й—Ё
жңҖеҗҺ пјҢ жҲ‘们еұ•зӨәйҮҸеӯҗеӣҙж Ҹзҡ„дёҖзұ»еҸҜиғҪзҡ„еә”з”Ё пјҢ жҲ–иҖ…иҜҙеұ•зӨәдёҖдёӘеҹәдәҺйҮҸеӯҗеӣҙж Ҹзҡ„йҮҸеӯҗдҝЎжҒҜеҺҹеһӢеҷЁд»¶ гҖӮ и®ҫ计并еҲ¶йҖ иҝҷж ·зҡ„еҷЁд»¶ пјҢ дҪҝд№ӢиғҪеӨҹе·ҘдҪңе’Ңе®һз”Ё пјҢ жүҚжҳҜжҲ‘们зү©зҗҶдәәеҜ№ж¶Ҳиҙ№зәізЁҺдәәеҠіеҠЁзҡ„еӣһжҠҘ гҖӮ
зәізұіеӣҙж Ҹдёӯзҡ„йҮҸеӯҗе°әеҜёж•Ҳеә”并йқһеҸӘжҳҜйҳіжҳҘзҷҪйӣӘ пјҢ еҸҜд»Ҙз”ЁжқҘжһ„йҖ еҺҹеӯҗеұӮж¬Ўзҡ„йҖ»иҫ‘й—ЁеҷЁд»¶ гҖӮ иҝҷдёҖеҷЁд»¶жӯЈжҳҜеҹәдәҺдёҠдёҖиҠӮзҡ„вҖңиҝ‘и—Өзі»з»ҹвҖқ延伸еҮәжқҘ гҖӮ Manoharan зӯүдәәеңЁ 2000 е№ҙе·ҰеҸіи§ӮжөӢеҲ°иҜұдәәзҡ„иҝ‘и—Өе…ұжҢҜйҮҸеӯҗжө·еёӮиңғжҘјзҺ°иұЎ пјҢ еұ•зӨәдәҶзәізұіе°әеәҰдёӢдҝЎжҒҜдј иҫ“зҡ„еҸҜиғҪжҖ§ гҖӮ 然иҖҢ пјҢ еҹәдәҺиҝ‘и—Өж•Ҳеә”зҡ„йҮҸеӯҗжө·еёӮиңғжҘјеҸӘеӯҳеңЁдәҺиҙ№зұіиғҪйҷ„иҝ‘ гҖӮ жңҖиҝ‘ пјҢ е®һйӘҢи§ӮжөӢеҲ° пјҢ дёҚдҫқиө–дәҺиҝ‘и—Өж•Ҳеә”д№ҹеҸҜд»Ҙжһ„йҖ еҮәйҮҸеӯҗжө·еёӮиңғжҘј пјҢ дё”иҝҷдёҖж•Ҳеә”жңүзӣёеҜ№иҫғй«ҳзҡ„дҝЎжҒҜдј иҫ“ж•ҲзҺҮгҖҒиғҪеңЁдёҖдёӘиҫғе®ҪиғҪйҮҸиҢғеӣҙеҶ…иҝӣиЎҢж“ҚжҺ§ гҖӮ еҲ©з”ЁиҝҷдәӣдјҳзӮ№ пјҢ еҺҹеӯҗе°әеәҰдёӢзҡ„йҖ»иҫ‘й—Ёе°ұжҲҗдёәеҸҜиғҪ пјҢ иҜёеҰӮвҖңйқһй—ЁвҖқгҖҒвҖңжүҮеҮәй—ЁвҖқдёҺвҖңжҲ–й—ЁвҖқеҚіеҸҜжһ„е»әеҮәжқҘ гҖӮ иҜҰз»ҶеҶ…е®№еҸҜи§Ғж–ҮзҢ® [Nature Commun. 11, 1400 (2020)] гҖӮ
иҝҷйҮҢзҡ„и®ҫи®ЎжҖқи·ҜеҰӮдёӢпјҡ
(1) жӨӯеңҶеһӢеӣҙж Ҹзҡ„з„ҰзӮ№дҪңдёәдҝЎжҒҜиҫ“е…Ҙе’Ңиҫ“еҮәз«Ҝ пјҢ е…¶дёӯиҫ“е…Ҙ вҖң1вҖқ / вҖң0вҖқ еҜ№еә”дәҺжӨӯеңҶзәізұіеӣҙж Ҹзҡ„дёҖдёӘз„ҰзӮ№еӨ„еҺҹеӯҗвҖңжңүвҖқ/вҖңж— вҖқ пјҢ иҖҢиҫ“еҮә вҖң1вҖқ / вҖң0вҖқ еҲҷйҖҡиҝҮеҸҰеӨ–дёҖдёӘз„ҰзӮ№еӨ„иҜұеҸ‘зҡ„йҮҸеӯҗиңғжҘјд№Ӣжү«жҸҸйҡ§йҒ“и°ұејәеәҰй«ҳ/дҪҺеҖјжқҘиЎЁзҺ° гҖӮ
(2) вҖңйқһй—ЁвҖқжҳҜдёҖдёӘдёӨз«Ҝз»“жһ„ пјҢ жӯЈеҘҪеҜ№еә”зқҖжӨӯеңҶзәізұіеӣҙж Ҹдёӯзҡ„еҸҚиҪ¬йҮҸеӯҗжө·еёӮиңғжҘј гҖӮ
(3) иҰҒе®һзҺ°вҖңжүҮеҮәй—ЁвҖқе’ҢвҖңжҲ–й—ЁвҖқ пјҢ йңҖиҰҒжһ„йҖ дёҖдёӘдёүз«Ҝз»“жһ„ гҖӮ иҝҷз§Қдёүз«Ҝз»“жһ„д№ҹи®ёжңүеҫҲеӨҡж–№жЎҲжқҘжһ„е»ә пјҢ дҪҶжңҖз®ҖеҚ•зҡ„ж–№жЎҲжҳҜйҖҡиҝҮз»„еҗҲдёӨдёӘжӨӯеңҶеӣҙж ҸжқҘе®һзҺ° пјҢ иҝҷдёӨдёӘжӨӯеңҶе…ұз”ЁдёҖдёӘз„ҰзӮ№ пјҢ д»ҺиҖҢжһ„жҲҗдёҖдёӘе“‘й“ғеһӢзҡ„еӣҙж Ҹ гҖӮ еӣҫ 9(a) жүҖзӨәеҚідёәиҝҷдёҖжҰӮеҝөдёӢзҡ„вҖңжүҮеҮәй—ЁвҖқ пјҢ е…¶дёӯдёӨдёӘжӨӯеңҶеӣҙж Ҹзҡ„е…ұеҗҢз„ҰзӮ№ A еӨ„еҺҹеӯҗвҖңж— вҖқ / вҖңжңүвҖқеҲҶеҲ«еҜ№еә”зқҖиҫ“е…Ҙ вҖң0вҖқ е’Ң вҖң1вҖқпјҢ еҰӮеӣҫ 9(a) жҳҫзӨә A еӨ„вҖңж— вҖқ пјҢ еҰӮеӣҫ 9(c) жҳҫзӨә A еӨ„вҖңжңүвҖқ гҖӮ иҖҢиҫ“еҮәзҡ„еҲҶеҲ«жҳҜз„ҰзӮ№ B е’Ң C еӨ„зҡ„жү«жҸҸйҡ§йҒ“и°ұж•°еҖјеӨ§е°Ҹ пјҢ еҰӮеӣҫ 9(b) е’Ң 9(d) жүҖзӨә гҖӮ еҪ“ A еӨ„жІЎжңүеҺҹеӯҗж—¶ (иҫ“е…Ҙдёә вҖң0вҖқ) пјҢ иҫ“еҮә B е’Ң C еӨ„зҡ„жү«жҸҸйҡ§йҒ“и°ұеҖјеҫҲдҪҺ (иҫ“еҮәдёә вҖң0вҖқ)пјӣеҪ“ A еӨ„жңүеҺҹеӯҗж—¶ (иҫ“е…Ҙдёә вҖң1вҖқ) пјҢ иҫ“еҮә B е’Ң C еӨ„зҡ„жү«жҸҸйҡ§йҒ“и°ұеҖјеҫҲй«ҳ (иҫ“еҮәдёә вҖң1вҖқ) гҖӮ иҝҷж · пјҢ иҫ“еҮәдёҺиҫ“е…Ҙж»Ўи¶івҖңжүҮеҮәй—ЁвҖқеҮҪж•°е…ізі» гҖӮ
жҺЁиҚҗйҳ…иҜ»
- дәәеӨ§йҷ„дёӯ|第37еұҠе…ЁеӣҪдёӯеӯҰз”ҹзү©зҗҶз«һиөӣеҢ—дә¬иөӣеҢәиҺ·еҘ–еҗҚеҚ•е…¬еёғ
- дјҠз“Ұе°”В·иҙҫеҹғеј—|вҖңзү©зҗҶеҮ д№ҺдёҚеҸҠж јзҡ„еҸ°зҗғйҖүжүӢвҖқпјҡдјҠз“Ұе°”В·иҙҫеҹғеј—
- иҺұеӣ е“Ҳеҫ·|вҖңеҰӮжһңеҶҚж—©еҮ е№ҙпјҢйңҚйҮ‘еә”иҜҘд№ҹиғҪеҫ—иҜәеҘ–вҖқ& 2020иҜәиҙқе°”зү©зҗҶеӯҰеҘ–
- е№ҝд№үзӣёеҜ№и®ә|2020е№ҙиҜәиҙқе°”зү©зҗҶеӯҰеҘ–жқғеЁҒи§ЈиҜ»пјҢдҪ жғізҹҘйҒ“зҡ„йғҪеңЁиҝҷйҮҢпјҒ
- GolevkaBao|е®Үе®ҷеӨ§зҲҶзӮёеҸҲжңүж–°еҸ‘зҺ°пјҹзү©зҗҶеӯҰ家и§ӮжөӢеҲ°е®Үе®ҷејҰж–°иҝ№иұЎпјҢдҪҶд»ҚйңҖиҜҒе®һ
- иҜәиҙқе°”зү©зҗҶеӯҰеҘ–|иҜәиҙқе°”зү©зҗҶеӯҰеҘ–е…¬еёғпјҒдёүдәәиҺ·еҘ–пјҢеҢ…жӢ¬дёҖеҗҚеҘіеӨ©ж–ҮеӯҰ家
- |еҫ·еӣҪ科еӯҰ家иҺ·иҜәиҙқе°”зү©зҗҶеӯҰеҘ– й»ҳе…Ӣе°”иЎЁзӨәзҘқиҙә
- иҜәиҙқе°”зү©зҗҶеӯҰеҘ–|еҲҡеҲҡпјҢ2020е№ҙиҜәиҙқе°”зү©зҗҶеӯҰеҘ–жҸӯжҷ“пјҒ
- зү©зҗҶ|2020зү©зҗҶиҜәеҘ–ж„ҸеӨ–еҘ–з»ҷй»‘жҙһпјҢ专家称早иҜҘеҫ—
- зү©зҗҶ|и§ЈиҜ»2020е№ҙиҜәиҙқе°”зү©зҗҶеҘ–пҪң他们жүҫеҲ°дәҶе®Үе®ҷдёӯжңҖеҘҮејӮзҡ„з§ҳеҜҶ











