зү©зҗҶ|еӣҡзҰҒдәҺзәізұіеӣҙж Ҹдёӯзҡ„йҮҸеӯҗ( дә” )
(3) зҡ„зЎ® пјҢ йҳөеҲ—дёӯдёҚеҗҢеӣҙж ҸдёӯеӯҳеңЁзҡ„ Gd еҺҹеӯҗж•°зӣ®жңүеҫҲеӨ§ж¶ЁиҗҪ пјҢ еҰӮеӣҫ 7(a) жүҖзӨә гҖӮ
(4) еҰӮжһңеӣҙж Ҹе°әеҜёи¶іеӨҹеӨ§гҖҒGd еҺҹеӯҗж•°и¶іеӨҹеӨҡ пјҢ йӮЈеӣҙж ҸеҶ… Gd еҺҹеӯҗж•°зҡ„ж¶ЁиҗҪзӣёеҜ№еҖје°ұдёҚжҳҫи‘— гҖӮ йҡҸзқҖеӣҙж Ҹе°әеҜёеҮҸе°ҸеҲ°зӣҙеҫ„еҸӘжңүзәізұіе°әеәҰ пјҢ Gd еҺҹеӯҗж•°е°‘ пјҢ ж¶ЁиҗҪе°ұйқһеёёжҳҫи‘— пјҢ еҰӮеӣҫ 7(a) жүҖзӨәе·ҰдёӢи§’зҡ„дёҖдёӘеӣҙж ҸеҶ…е°ұжҳҜз©әзҡ„ гҖӮ
зҡ„зЎ® пјҢ з”ұдәҺйҮҸеӯҗеӣҙж Ҹжһ„е»әдәҶдёҖдёӘеҫҲй«ҳзҡ„еҠҝеһ’ пјҢ еӣҙж ҸеҶ…зҡ„ Gd еҺҹеӯҗеҚідҫҝжүҫдёҚеҲ°иғҪйҮҸеҫҲдҪҺзҡ„дҪҚзҪ® пјҢ дҪҶд№ҹж— жі•йҖғйҖёеҮәеӣҙж Ҹ пјҢ иҖҢеӨ–йқўзҡ„еҺҹеӯҗд№ҹж— жі•еҒ·жёЎи¶Ҡеўғиҝӣе…Ҙеӣҙж Ҹ гҖӮ иҝҷжүҚжҳҜ Gd еҺҹеӯҗж•°еұ•зҺ°е·ЁеӨ§ж¶ЁиҗҪзҡ„еҺҹеӣ гҖӮ йӮЈд№ҲжҖҺд№ҲиғҪеӨҹжҠ‘еҲ¶иҝҷз§Қж¶ЁиҗҪе‘ўпјҹжңҖз®ҖеҚ•зӣҙжҺҘзҡ„ж–№жі•дҫҝжҳҜе°Ҷеӣҙж Ҹжү“ејҖдёҖдёӘеҸЈеӯҗ пјҢ е…Ғи®ёиҮӘз”ұиҝӣеҮә пјҢ зңӢзңӢдјҡжҳҜжҖҺд№Ҳж ·зҡ„з»“жһң гҖӮ
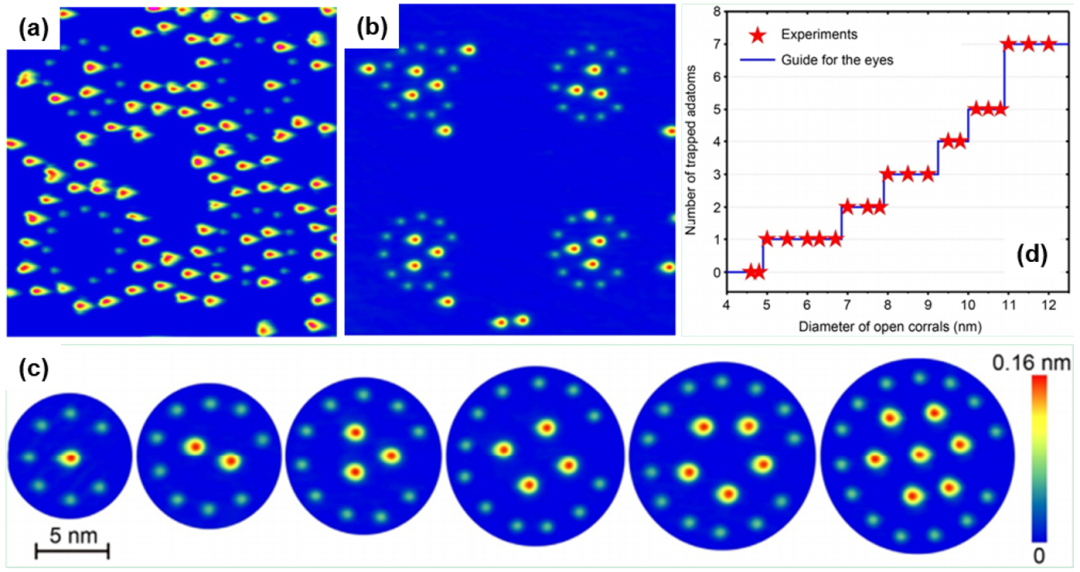
жһң然 пјҢ еҰӮжһңжһ„е»әдёҖдёӘеёҰејҖеҸЈзҡ„еӣҙж ҸйҳөеҲ— пјҢ жғ…еҪўе°ұеҸҳеҫ—жҲӘ然дёҚеҗҢ гҖӮ з•ҷдёҖдёӘејҖеҸЈ пјҢ е°ұиғҪе®һзҺ°еӣҙж ҸеҶ…еҺҹеӯҗж•°еҸҜжҺ§ пјҢ д№ҹе°ұжҳҜиҜҙиғҪжҠ‘еҲ¶з»ҹи®Ўж¶ЁиҗҪ гҖӮ еҰӮеӣҫ 7(b) жүҖзӨә пјҢ жүҖжңүеӣҙж ҸеҶ… Gd зҡ„ж•°зӣ®йғҪжҳҜ 3 дёӘ пјҢ ж„Ҹе‘ізқҖиҝҷдёӘе°әеҜё (зӣҙеҫ„ 8.5 nm) зҡ„еӣҙж ҸеҶ…е°ұеҸӘиғҪжүҝиҪҪ 3 дёӘ Gd еҺҹеӯҗеӯҳеңЁ гҖӮ иҝҷжҳҜйҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„з»қеҰҷдҪ“зҺ° пјҢ д»ӨдәәйңҮж…‘ пјҢ зӣёе…із»ҶиҠӮеҸҜеҸӮи§Ғж–ҮзҢ® [Phys. Rev. B 90, 045433 (2014)] гҖӮ
еҘҪпјҒзҺ°еңЁжқҘзңӢеӣҙж Ҹе°әеҜёж•Ҳеә” гҖӮ йҮҮз”ЁдёҚеҗҢзӣҙеҫ„зҡ„ејҖеҸЈеӣҙж Ҹ пјҢ еҸҜе®һзҺ°дёҚеҗҢ Gd еҺҹеӯҗж•°зӣ®зҡ„е®ҡйҮҸжҚ•иҺ· пјҢ еҰӮеӣҫ 7(c) жүҖзӨә гҖӮ еӣҙж Ҹи¶ҠеӨ§ пјҢ иғҪжҚ•иҺ·зҡ„ Gd еҺҹеӯҗж•°зӣ®и¶ҠеӨҡ пјҢ иҝҷжҳҜе…¶дёҖ гҖӮ е…¶дәҢ пјҢ еӣҙж ҸеҶ… Gd еҺҹеӯҗеҖҫеҗ‘дәҺжҺ’жҲҗжӯЈеӨҡиҫ№еҪў пјҢ 并且еӯҳеңЁеӣӣиҫ№еҪўе’Ңдә”иҫ№еҪўиҝҷж ·зҡ„жҳҺжҳҫдёҚеҗҢдәҺ Ag (111) иЎЁйқўе…ӯи§’жҷ¶ж јзҡ„еҪўзҠ¶ пјҢ иҝҷд№ҹиҜҒжҳҺеӣҙж ҸеҶ…зҡ„йҮҸеӯҗе°әеҜёж•Ҳеә” гҖӮ
дёәдәҶиҝӣдёҖжӯҘйӘҢиҜҒе®ҡйҮҸеҺҹеӯҗжҚ•иҺ·зҡ„зЁіе®ҡжҖ§ пјҢ жҲ‘们系з»ҹз ”з©¶дәҶејҖеҸЈеӣҙж Ҹзӣҙеҫ„дёҺжҚ•иҺ· Gd еҺҹеӯҗж•°зҡ„е…ізі» пјҢ еҰӮеӣҫ 7(d) жүҖзӨәпјҡGd еҺҹеӯҗж•°дёҺ Fe еӣҙж Ҹзӣҙеҫ„е‘ҲеҸ°йҳ¶зҠ¶ пјҢ 并且иҫғе®ҪеҸ°йҳ¶з»ҷдәҶиҫғеӨ§еӣҙж Ҹзӣҙеҫ„йҖүжӢ©з©әй—ҙе’Ңе®№й”ҷжҖ§ гҖӮ еҫҲжҳҫ然 пјҢ иҝҷж ·жјӮдә®зҡ„еҸ°йҳ¶з»“жһ„жҳҫзӨәдәҶз»“жһңзҡ„жҳҫи‘—жҖ§ пјҢ еҖјеҫ—д»”з»Ҷеӣһе‘і гҖӮ иҝҷйҮҢ пјҢ д»Өдәәз–‘жғ‘зҡ„жҳҜеӣҙж ҸжҚ•иҺ· 1гҖҒ2гҖҒ3гҖҒ4гҖҒ5гҖҒ7 дёӘ Gd еҺҹеӯҗзҡ„жғ…еҪўйғҪиў«и§ӮжөӢеҲ° пјҢ дҪҶжҚ•иҺ· 6 дёӘ Gd еҺҹеӯҗзҡ„жғ…еҪўжІЎжңүеҮәзҺ° гҖӮ д№ҹи®ёеҸҜд»Ҙиҝҷд№ҲжқҘзҗҶи§ЈпјҡеҰӮжһң 6 дёӘ Gd еҺҹеӯҗеңЁеӣҙж ҸеҶ…еҪўжҲҗдәҶжӯЈе…ӯиҫ№еҪў пјҢ з”ұдәҺ Gd вҖ“ Gd еҺҹеӯҗд№Ӣй—ҙжҳҜеҗёеј•еҠҝ пјҢ д»ҺиғҪйҮҸдёҠеә”иҜҘй©ұеҠЁз¬¬ 7 дёӘеҺҹеӯҗд»Һеӣҙж ҸеӨ–йғЁиҝӣе…ҘеҲ°е…ӯиҫ№еҪўдёӯеҝғ пјҢ дҪҝеҫ—дҪ“зі»жҖ»иғҪйҮҸжӣҙдҪҺ гҖӮ
иҝҷдёҖз»„з»“жһңиЎЁжҳҺиҮіе°‘дёӨзӮ№пјҡ
(1) д»Һе®һйӘҢе’ҢзҗҶи®әдёҠйӘҢиҜҒдәҶзІҫзЎ®еҸҜжҺ§зҡ„еҺҹеӯҗжҚ•иҺ·еҪ’еҠҹдәҺејҖеҸЈеӣҙж ҸдёӯйҮҸеӯҗе°әеҜёж•Ҳеә”дә§з”ҹзҡ„иҮӘжҲ‘и°ғиҠӮиҝҮзЁӢпјҡеҰӮжһңжҚ•иҺ·зҡ„ Gd еҺҹеӯҗж•°дёҚи¶і пјҢ еӣҙж ҸдјҡиҮӘеҸ‘ең°д»ҺеӨ–з•ҢжҚ•иҺ·еҺҹеӯҗ гҖӮ еҰӮжһңеӣҙж ҸеҶ…жңүдәҶиҝҮеӨҡеҺҹеӯҗ пјҢ еҲҷеӨҡдҪҷеҺҹеӯҗдјҡиў«жҺ’ж–ҘиҖҢйҖғйҖёеҮәеҺ» пјҢ д»ҺиҖҢе®һзҺ°еӣҙж Ҹе®ҡйҮҸжҚ•иҺ·еҺҹеӯҗзҡ„ж•Ҳеә” гҖӮ
(2) еә”з”ЁдёҠ пјҢ еҸҜеҲ©з”ЁдёҚеҗҢзӣҙеҫ„ејҖеҸЈеӣҙж ҸеҶ…зҡ„дәҢз»ҙйҮҸеӯҗе°әеҜёж•Ҳеә”жқҘжһ„е»әеҚ•еҺҹеӯҗзІҫеәҰзҡ„еҺҹеӯҗз»“жһ„ пјҢ е®һзҺ°жңҖеӨ§йҷҗеәҰжҠ‘еҲ¶еҺҹеӯҗж•°зӣ®з»ҹи®Ўж¶ЁиҗҪ пјҢ е®һзҺ°еұҖеҹҹз»“жһ„жҺ§еҲ¶ гҖӮ
жң¬ж–ҮеӣҫзүҮ
еӣҫ7. йҮҸеӯҗеӣҙж Ҹдёӯе°әеҜёж•Ҳеә”зҡ„ж¶ЁиҗҪдёҺжҠ‘еҲ¶ гҖӮ (a) Fe еҺҹеӯҗе°Ғй—ӯеӣҙж ҸйҳөеҲ—еҸҠе…¶еҶ…йғЁеӯҳеңЁзҡ„ Gd еҺҹеӯҗеӣҫеғҸ пјҢ жҳҫзӨәеҺҹеӯҗж•°зӣ®е·ЁеӨ§ж¶ЁиҗҪ пјҢ е·ҰдёӢи§’зҡ„еӣҙж ҸеҶ…з”ҡиҮіжІЎжңү Gd еҺҹеӯҗ гҖӮ (b) Fe еҺҹеӯҗзҡ„ејҖеҸЈеӣҙж ҸйҳөеҲ—еҸҠжҜҸдёӘеӣҙж ҸжҚ•иҺ·дәҶзӯүйҮҸзҡ„ Gd еҺҹеӯҗ (3 дёӘ) гҖӮ (c) дёҚеҗҢзӣҙеҫ„ејҖеҸЈеӣҙж ҸеҶ…зҡ„ Gd еҺҹеӯҗжҺ’еҲ— пјҢ е‘ҲзҺ°еҮәзӮ№гҖҒзәҝгҖҒдёүи§’еҪўгҖҒеӣӣиҫ№еҪўгҖҒдә”иҫ№еҪўе’ҢеҚ еҝғе…ӯиҫ№еҪўеҪўжҖҒ гҖӮ еӣҫдёӯйҮҸеӯҗеӣҙж Ҹз”ұе°Ҹзҡ„е®һеҝғдә®зӮ№зҰ»ж•ЈеңҶзҺҜ (Fe еҺҹеӯҗ) жһ„жҲҗгҖҒеӨ§зҡ„дә®зӮ№дёә Gd еҺҹеӯҗ гҖӮ (d) дёҚеҗҢе°әеҜёејҖеҸЈеӣҙж ҸдёӯжҚ•иҺ·дёҚеҗҢж•°зӣ®еҺҹеӯҗзҡ„еҸ°йҳ¶зҠ¶дҫқиө–е…ізі» пјҢ жіЁж„ҸжІЎжңү 6 дёӘеҺҹеӯҗзҡ„еҸ°йҳ¶ гҖӮ иҜҰз»ҶеҶ…е®№еҸӮиҖғж–ҮзҢ® [Phys. Rev. B 90, 045433 (2014)] гҖӮ
5. иҝ‘и—Өзү©зҗҶ
иЎҢж–ҮиҮіжӯӨзҡ„жүҖжңүйҮҸеӯҗе°әеҜёж•Ҳеә”е®һйӘҢ пјҢ жүҖе…іжіЁзҡ„иҝҳеҸӘжҳҜйҮҸеӯҗеӣҙж ҸдёӯеӨ–жқҘеҺҹеӯҗ (дҫӢеҰӮ Gd) дёҺ Ag (111) иЎЁйқўжҖҒзҡ„зӣёдә’дҪңз”Ё гҖӮ жӣҙж·ұеҲ»зҡ„зү©зҗҶз ”з©¶е·ҘдҪңиҝҳеҸҜд»ҘжңүеҫҲеӨҡ пјҢ дҫӢеҰӮеҮқиҒҡжҖҒзү©зҗҶдёӯзҹҘеҗҚзҡ„иҝ‘и—Ө (Kondo) ж•Ҳеә”еҚіеұһе…¶дёӯд№ӢдёҖ гҖӮ
дј—жүҖе‘ЁзҹҘ пјҢ иҝ‘и—Өж•Ҳеә”жҸҸиҝ°зҡ„жҳҜзЈҒжҖ§жқӮиҙЁзҡ„еұҖеҹҹиҮӘж—ӢдёҺдј еҜјз”өеӯҗд№Ӣй—ҙзҡ„иҮӘж—Ӣзӣёе…іж•Је°„ гҖӮ еңЁиҝ‘и—Өж•Ҳеә”дёӯ пјҢ жңүдёҖдёӘзү№еҫҒжё©еәҰвҖ”вҖ”иҝ‘и—Өжё©еәҰ пјҢ е®ғиғҪеӨҹеҸҚжҳ зЈҒжҖ§жқӮиҙЁзҡ„зЈҒжҖ§зҠ¶жҖҒ гҖӮ иҝҷйҮҢдёәдәҶж–№дҫҝиҜҙжҳҺй—®йўҳ пјҢ 姑且еҒҮи®ҫзЈҒжҖ§жқӮиҙЁиҮӘж—Ӣ S = 1/2 (еҪ“然 пјҢ иҝ‘и—Өж•Ҳеә”жүҖжҸҸиҝ°зҡ„зЈҒжҖ§жқӮиҙЁиҮӘж—Ӣ并дёҚеұҖйҷҗдәҺ S = 1/2 ) гҖӮ еҪ“зі»з»ҹжё©еәҰиҝңдҪҺдәҺиҝ‘и—Өжё©еәҰж—¶ пјҢ зЈҒжҖ§жқӮиҙЁдёҺе‘Ёеӣҙдј еҜјз”өеӯҗеҸ‘з”ҹзҡ„иҮӘж—Ӣзӣёе…іж•Је°„иҫғејә пјҢ еҪўжҲҗдёҖдёӘеӨҡдҪ“ж•Ҳеә”зҡ„иҮӘж—ӢеҚ•жҖҒ пјҢ еҚі S = 0 гҖӮ йҖҡдҝ—зҡ„зҗҶи§ЈдәҰеҸҜз§°д№ӢдёәзЈҒжҖ§жқӮиҙЁиҮӘж—Ӣиў«еұҸи”ҪжҺүдәҶ гҖӮ еҪ“зі»з»ҹжё©еәҰиҝңй«ҳдәҺиҝ‘и—Өжё©еәҰж—¶ пјҢ зЈҒжҖ§жқӮиҙЁдёҺе‘Ёеӣҙдј еҜјз”өеӯҗеҸ‘з”ҹзҡ„иҮӘж—Ӣзӣёе…іж•Је°„иҫғејұ пјҢ жӯӨж—¶еӨҡдҪ“иҮӘж—ӢеҚ•жҖҒж— жі•еҪўжҲҗ пјҢ жқӮиҙЁиҮӘж—Ӣдҫқ然еӯҳеңЁ гҖӮ д»ҺиҝҷдёӘж„Ҹд№үдёҠзңӢ пјҢ жүҖи°“вҖңиҝ‘и—Өжё©еәҰвҖқд№ҹе°ұжҳҜдёҖдёӘиғҪйҮҸе°әеәҰ пјҢ иЎЎйҮҸдәҶзЈҒжҖ§жқӮиҙЁеұҖеҹҹиҮӘж—ӢдёҺдј еҜјз”өеӯҗд№Ӣй—ҙиҮӘж—Ӣзӣёе…іж•Је°„зҡ„ејәејұ гҖӮ
д№ҹеҫҲжҳҫ然 пјҢ еҰӮжһңжҲ‘们еҸҜд»ҘжңүеҠһжі•и°ғжҺ§дј еҜјз”өеӯҗзҡ„жө“еәҰ пјҢ д№ҹе°ұеҸҜд»Ҙи°ғжҺ§жӯӨзұ»иҮӘж—Ӣзӣёе…іж•Је°„ гҖӮ з”өеӯҗжө“еәҰи¶Ҡй«ҳ пјҢ е°ұи¶Ҡе®№жҳ“еұҸи”ҪзЈҒжҖ§жқӮиҙЁзҡ„иҮӘж—Ӣ гҖӮ иҝҷе°ұжҳҜзү©зҗҶдәәз»Ҹеёёи®Ёи®әзҡ„вҖңзЈҒжҖ§жқӮиҙЁзҡ„иҮӘж—ӢеұҸи”ҪдёҺиҙ№зұіиғҪзә§еӨ„зҡ„з”өеӯҗжө“еәҰ (д№ҹе°ұжҳҜжҖҒеҜҶеәҰ) еҜҶеҲҮзӣёе…івҖқзҡ„йҖҡдҝ—иҜҙиҫһ гҖӮ жҚўеҸҘиҜқиҜҙ пјҢ иҝ‘и—Өжё©еәҰеҝ…е®ҡдёҺж ·е“Ғзҡ„иҙ№зұійқўеӨ„жҖҒеҜҶеәҰеҜҶеҲҮзӣёе…іпјҡжҖҒеҜҶеәҰи¶Ҡй«ҳ пјҢ еҲҷиҝ‘и—Өж•Ҳеә”дёӯзҡ„иҝ‘и—Өжё©еәҰе°ұи¶Ҡй«ҳ гҖӮ и°ғжҺ§жҖҒеҜҶеәҰ пјҢ еҚіеҸҜи°ғжҺ§иҝ‘и—Өжё©еәҰ гҖӮ
жҺЁиҚҗйҳ…иҜ»
- дәәеӨ§йҷ„дёӯ|第37еұҠе…ЁеӣҪдёӯеӯҰз”ҹзү©зҗҶз«һиөӣеҢ—дә¬иөӣеҢәиҺ·еҘ–еҗҚеҚ•е…¬еёғ
- дјҠз“Ұе°”В·иҙҫеҹғеј—|вҖңзү©зҗҶеҮ д№ҺдёҚеҸҠж јзҡ„еҸ°зҗғйҖүжүӢвҖқпјҡдјҠз“Ұе°”В·иҙҫеҹғеј—
- иҺұеӣ е“Ҳеҫ·|вҖңеҰӮжһңеҶҚж—©еҮ е№ҙпјҢйңҚйҮ‘еә”иҜҘд№ҹиғҪеҫ—иҜәеҘ–вҖқ& 2020иҜәиҙқе°”зү©зҗҶеӯҰеҘ–
- е№ҝд№үзӣёеҜ№и®ә|2020е№ҙиҜәиҙқе°”зү©зҗҶеӯҰеҘ–жқғеЁҒи§ЈиҜ»пјҢдҪ жғізҹҘйҒ“зҡ„йғҪеңЁиҝҷйҮҢпјҒ
- GolevkaBao|е®Үе®ҷеӨ§зҲҶзӮёеҸҲжңүж–°еҸ‘зҺ°пјҹзү©зҗҶеӯҰ家и§ӮжөӢеҲ°е®Үе®ҷејҰж–°иҝ№иұЎпјҢдҪҶд»ҚйңҖиҜҒе®һ
- иҜәиҙқе°”зү©зҗҶеӯҰеҘ–|иҜәиҙқе°”зү©зҗҶеӯҰеҘ–е…¬еёғпјҒдёүдәәиҺ·еҘ–пјҢеҢ…жӢ¬дёҖеҗҚеҘіеӨ©ж–ҮеӯҰ家
- |еҫ·еӣҪ科еӯҰ家иҺ·иҜәиҙқе°”зү©зҗҶеӯҰеҘ– й»ҳе…Ӣе°”иЎЁзӨәзҘқиҙә
- иҜәиҙқе°”зү©зҗҶеӯҰеҘ–|еҲҡеҲҡпјҢ2020е№ҙиҜәиҙқе°”зү©зҗҶеӯҰеҘ–жҸӯжҷ“пјҒ
- зү©зҗҶ|2020зү©зҗҶиҜәеҘ–ж„ҸеӨ–еҘ–з»ҷй»‘жҙһпјҢ专家称早иҜҘеҫ—
- зү©зҗҶ|и§ЈиҜ»2020е№ҙиҜәиҙқе°”зү©зҗҶеҘ–пҪң他们жүҫеҲ°дәҶе®Үе®ҷдёӯжңҖеҘҮејӮзҡ„з§ҳеҜҶ











