зү©зҗҶ|еӣҡзҰҒдәҺзәізұіеӣҙж Ҹдёӯзҡ„йҮҸеӯҗ( дёү )
д»ҺиҝҷдёӘж„Ҹд№үдёҠ пјҢ йҮҸеӯҗеӣҙж Ҹе°ұжҲҗдёәз ”з©¶йҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„жӢ©дјҳеҜ№иұЎд№ӢдёҖзұ» гҖӮ еҺҹеӣ ж— д»– пјҢ еҚі STM й…ҚеҗҲйҮҸеӯҗеӣҙж Ҹ пјҢ еҸҜд»ҘйҡҸж„ҸеҲ¶йҖ еҗ„з§ҚйҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„еңәжҷҜ пјҢ 然еҗҺе®һең°иЎЁеҫҒйҮҸеӯҗеӣҙж Ҹдёӯзҡ„еҗ„з§ҚйҮҸеӯҗе№Іж¶үгҖҒзә зј гҖҒе…іиҒ”е’Ңе…¶д»–зӣёе…іж•Ҳеә” гҖӮ жҠҖжңҜдёҠ пјҢ иҝҷз§Қз ”з©¶еҸӘйңҖ STM дёҖеҘ—гҖҒе·§жүӢдёҖеҸҢгҖҒжңүиҖҗеҝғзҡ„и„‘иўӢдёҖжһҡ пјҢ дҫҝеҸҜд»ҘеңЁ CuгҖҒAg зӯү (111) йқўдёҠжҢүз…§ Go вҖ“ Go вҖ“ Go зҡ„жЁЎејҸдёӢеӣҙжЈӢ пјҢ д»ҺиҖҢдёӢеҮәеҚғдёҮз§ҚеҸҳеҢ–гҖҒеҚғдёҮз§ҚжҪ®жөҒгҖҒз”ҡиҮіжҳҜе®Үе®ҷжөҒ гҖӮ
4. еӣҡзҰҒдәҺеӣҙж Ҹзҡ„йҮҸеӯҗ
зү©зҗҶдёҠ пјҢ йҖҡеёёж №жҚ®е°әеҜёйҮҸеӯҗеҢ–зҡ„з»ҙж•° пјҢ е°ҶйҮҸеӯҗе°әеҜёж•Ҳеә”еҲҶдёәдёүзұ»пјҡ
(1) дёҖз»ҙеҸ—йҷҗи¶…и–„иҶң (жҢҮи–„иҶңеҺҡеәҰж–№еҗ‘) гҖӮ
(2) дәҢз»ҙеҸ—йҷҗзәізұіеӣҙж Ҹе’ҢеІӣ (е№ійқўеҶ…еҸ—йҷҗе°әеҜё) гҖӮ
(3) дёүз»ҙеҸ—йҷҗйҮҸеӯҗзӮ№ (дёүз»ҙеҸ—йҷҗ) гҖӮ
дёҖз»ҙи–„иҶңдёӯйҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„е®һйӘҢиғҪеӨҹиҝҪжәҜеҲ° 1966 е№ҙ гҖӮ еҪ“ж—¶еҸ‘зҺ°еңЁй“Ӣ (Bi) и¶…и–„иҶңдёӯ пјҢ з”өйҳ»зҺҮгҖҒйңҚе°”зі»ж•°е’ҢзЈҒз”өйҳ»еқҮе‘ҲзҺ°еҮәеҺҡеәҰдҫқиө–зҡ„зҺ°иұЎ пјҢ иҖҢе®Ҹи§ӮдёҠиҝҷдәӣжҖ§иҙЁеә”иҜҘдёҺеҺҡеәҰж— е…і гҖӮ жӯӨеҗҺ пјҢ и–„иҶңдёӯйҮҸеӯҗе°әеҜёж•Ҳеә”иў«жӢ“еұ•еҲ°е…үеӯҰгҖҒзӣёеҸҳгҖҒи¶…еҜје’ҢзЈҒжҖ§зӯүйўҶеҹҹ гҖӮ еә”з”Ёж–№йқў пјҢ и–„иҶңйҮҸеӯҗе°әеҜёж•Ҳеә”иғҪеӨҹз”ЁжқҘж”№еҸҳзЈҒжҖ§и–„иҶңеұӮй—ҙиҖҰеҗҲдҪңз”Ё пјҢ 并и°ғжҺ§е·ЁзЈҒйҳ» гҖӮ еҜ№йҮҸеӯҗзӮ№дёӯдёүз»ҙйҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„з ”з©¶е§ӢдәҺ 1980 е№ҙд»Јжң« гҖӮ йҮҸеӯҗзӮ№еңЁеҢ»еӯҰе’ҢеұҸ幕жҳҫзӨәдёҠеқҮжңүе№ҝжіӣеә”з”Ё гҖӮ жӯӨеӨ– пјҢ еңЁе®һзҺ°йҮҸеӯҗи®Ўз®—зҡ„йҒ“и·ҜдёҠ пјҢ йҮҸеӯҗзӮ№д№ҹжҸҗдҫӣдәҶдёҖз§ҚеҸҜдҫӣйҖүжӢ©зҡ„жҠҖжңҜж–№жЎҲ гҖӮ иҮідәҺдәҢз»ҙе№ійқўйҮҸеӯҗеҸ—йҷҗж•Ҳеә”зҡ„е…іжіЁеҲҷдёҺеҷЁд»¶е°ҸеһӢеҢ–жңүеҜҶеҲҮе…іиҒ” пјҢ жүҖд»Ҙ IBM иҝҷж ·зҡ„е•Ҷдёҡе…¬еҸёжүҚдјҡеҜ№жӯӨйўҮж„ҹе…ҙи¶Ј гҖӮ еҰӮеӣҫ 4 жүҖзӨә пјҢ 笔иҖ…еңЁиҝҷйҮҢе°Ҷдё»иҰҒи®Ёи®әзәізұійҮҸеӯҗеӣҙж Ҹдёӯзҡ„дәҢз»ҙйҮҸеӯҗе°әеҜёж•Ҳеә” [1] гҖӮ
еҰӮеүҚжүҖиҝ° пјҢ еҜ№йҮҸеӯҗеӣҙж Ҹе°әеҜёж•Ҳеә”зҡ„ејҖеҲӣжҖ§з ”究йҷӨдәҶеӣҫ 1 жүҖзӨәзҡ„з”өеӯҗжҖҒйҮҸеӯҗжқҹзјҡ пјҢ иҝҳжңүиҝ‘и—Өе…ұжҢҜзҡ„йҮҸеӯҗжө·еёӮиңғжҘјж•Ҳеә” гҖӮ йҷӨжӯӨд№ӢеӨ– пјҢ йҮҸеӯҗе°әеҜёж•Ҳеә”д№ҹиў«з”ЁжқҘеј•еҜјеҺҹеӯҗжү©ж•ЈдёҺиҮӘз»„з»ҮгҖҒжҺ§еҲ¶з»ҹи®Ўж¶ЁиҗҪе’Ңи°ғеҲ¶иҝ‘и—Өжё©еәҰ гҖӮ жңҖиҝ‘зҡ„з ”з©¶е·ҘдҪңиЎЁжҳҺ пјҢ дёҚдҫқиө–дәҺиҝ‘и—Өж•Ҳеә”зҡ„йҮҸеӯҗжө·еёӮиңғжҘјж•Ҳеә”иғҪеӨҹеңЁиҙ№зұіиғҪйҷ„иҝ‘иҫғе®Ҫзҡ„иғҪйҮҸиҢғеӣҙеҶ…еӯҳеңЁ пјҢ еј•иө·е№ҝжіӣе…іжіЁ гҖӮ жӣҙйҮҚиҰҒзҡ„жҳҜ пјҢ дёҺиҝ‘и—Өж— е…ізҡ„йҮҸеӯҗжө·еёӮиңғжҘјдҝЎеҸ·з”ҡиҮіиғҪеӨҹжҜ”еҺҹзү©жҖҒзҡ„дҝЎеҸ·жӣҙејә пјҢ йўҮжңүдәӣж— дёӯз”ҹжңүзҡ„е‘ійҒ“ гҖӮ еҹәдәҺиҝҷдәӣдјҳзӮ№ пјҢ зү©зҗҶдәәи®ҫжғіеҖҹеҠ©дәҺж“ҚзәөдёҺиҝ‘и—Өж— е…ізҡ„йҮҸеӯҗжө·еёӮиңғжҘј пјҢ еҸҜиғҪе®һзҺ°еҹәжң¬йҖ»иҫ‘й—Ё пјҢ дҫӢеҰӮвҖңйқһй—ЁвҖқгҖҒвҖңжүҮеҮәй—ЁвҖқеҸҠвҖңжҲ–й—ЁвҖқзӯү гҖӮ иҝҷйҮҢжңүи¶Јзҡ„жҖқи·ҜжҳҜпјҡжө·еёӮиңғжҘјжң¬жқҘе°ұжҳҜж— дёӯз”ҹжңү пјҢ зҺ°еңЁз«ҹ然еҸҜд»Ҙз”Ёж— дёӯз”ҹжңүжқҘе®һзҺ°зңҹе®һзҡ„еҠҹиғҪ пјҢ жҳҜеҗҰжңүжө·еёӮиңғжҘјзҡ„ж„ҹи§үпјҒ
дёҚеҰЁжқҘзңӢеҮ дёӘдҫӢеӯҗ пјҢ зңӢзңӢзү©зҗҶдәәжҳҜеҰӮдҪ•з”ЁвҖңжө·еёӮиңғжҘјвҖқжқҘе®һзҺ°зү©зҗҶеҠҹиғҪзҡ„ гҖӮ иҝҷдәӣдҫӢеӯҗдё»иҰҒеҮәиҮӘ笔иҖ…иҝҮеҺ»иӢҘе№Іе№ҙжқҘзҡ„ж‘ёзҙўжҖ§з ”究数жҚ® пјҢ иҷҪ然结жһңжҳҫеҫ—иҝҳеҫҲз®ҖйҷӢе’ҢеҲқжӯҘ гҖӮ
жң¬ж–ҮеӣҫзүҮ
еӣҫ4. зәізұійҮҸеӯҗеӣҙж ҸдёӯйҮҸеӯҗе°әеҜёж•Ҳеә”зӨәж„ҸеӣҫеҸҠе…іиҒ”з ”з©¶зӨәж„Ҹеӣҫ [1] гҖӮ
4.1. еҺҹеӯҗжү©ж•Ј
第дёҖдёӘдҫӢеӯҗжҳҜеҺҹеӯҗеңЁеӣҙж ҸеҶ…жү©ж•ЈиЎҢдёәзҡ„йҮҸеӯҗйҷҗеҹҹж•Ҳеә” гҖӮ
иЎЁйқўзү©зҗҶеҫҲж—©е°ұе‘ҠиҜүжҲ‘们 пјҢ жҷ¶дҪ“иЎЁйқўеҰӮжһңеӯҳеңЁдёҖдёӘеҺҹеӯҗ пјҢ еҸӘиҰҒиөӢдәҲе…¶и¶іеӨҹеҠЁиғҪ пјҢ е®ғе°ұдјҡеңЁиЎЁйқўиҝӣиЎҢж— и§„йҡҸжңәиЎҢиө° гҖӮ жӯӨдёәз»Ҹе…ёеҺҹеӯҗжү©ж•ЈиЎҢдёә пјҢ зұ»жҜ”дәҺе®Ҹи§Ӯзҡ„еёғжң—иҝҗеҠЁиЎҢдёә гҖӮ жҖҺд№ҲиғҪеӨҹеңЁйқўеҝғз«Ӣж–№йҮ‘еұһ (111) иЎЁйқўдёҠзҡ„йҮҸеӯҗеӣҙж Ҹдёӯе®һзҺ°жү©ж•ЈиЎҢдёәзҡ„и§ӮжөӢе‘ўпјҹжңҖз®ҖеҚ•зӣҙжҺҘзҡ„еҒҡжі•жҳҜпјҡ
(1) йҖүжӢ©дёҖдёӘеҗҲйҖӮзҡ„йҮ‘еұһ (111) иЎЁйқў гҖӮ иҝҷйҮҢйҖүжӢ© Ag иҖҢдёҚжҳҜ Cu зҡ„ (111) йқўдҪңдёәиЎЁйқўпјӣ
(2) йҖүжӢ©дёҖдёӘе®һйӘҢжё©еәҰ пјҢ дёҖиҲ¬жҳҜж¶Іж°Ұжё©еәҰпјӣ
(3) йҖүжӢ©дёҖзұ»йҮ‘еұһеҺҹеӯҗеңЁ Ag (111) иЎЁйқўжһ„е»әйҮҸеӯҗеӣҙж Ҹ гҖӮ жіЁж„Ҹ пјҢ жһ„е»әеӣҙж Ҹзҡ„еҺҹеӯҗеҝ…йЎ»и¶іеӨҹзЁіе®ҡ пјҢ дёҚиғҪеҲ°еӨ„иЎҢиө° гҖӮ еҸҜд»ҘжҢ‘йҖү Fe еҺҹеӯҗз»„е»әеӣҙж Ҹ пјҢ еӣ дёә Ag (111) иЎЁйқўдёҠзҡ„ Fe еҺҹеӯҗжү©ж•ЈеҠҝеһ’иҫғй«ҳ пјҢ еңЁж¶Іж°Ұжё©еәҰдёӢдҪҚзҪ®и¶іеӨҹзЁіе®ҡпјӣ
(4) йҖүжӢ©дёҖзұ»йҮ‘еұһеҺҹеӯҗдҪңдёәжү©ж•ЈзӨәиёӘеҺҹеӯҗ гҖӮ иҝҷз§ҚеҺҹеӯҗеңЁ Ag (111) иЎЁйқўдёҠеә”иҜҘеҫҲе®№жҳ“йҡҸжңәжү©ж•Ј пјҢ еҚіжү©ж•ЈеҠҝеһ’еҫҲдҪҺ гҖӮ еҰӮ Gd еҺҹеӯҗеңЁж¶Іж°Ұжё©еәҰдёӢе…¶иЎЁйқўжү©ж•ЈиғҪеҠӣдҫқ然еҫҲејә гҖӮ
жң¬ж–ҮеӣҫзүҮ
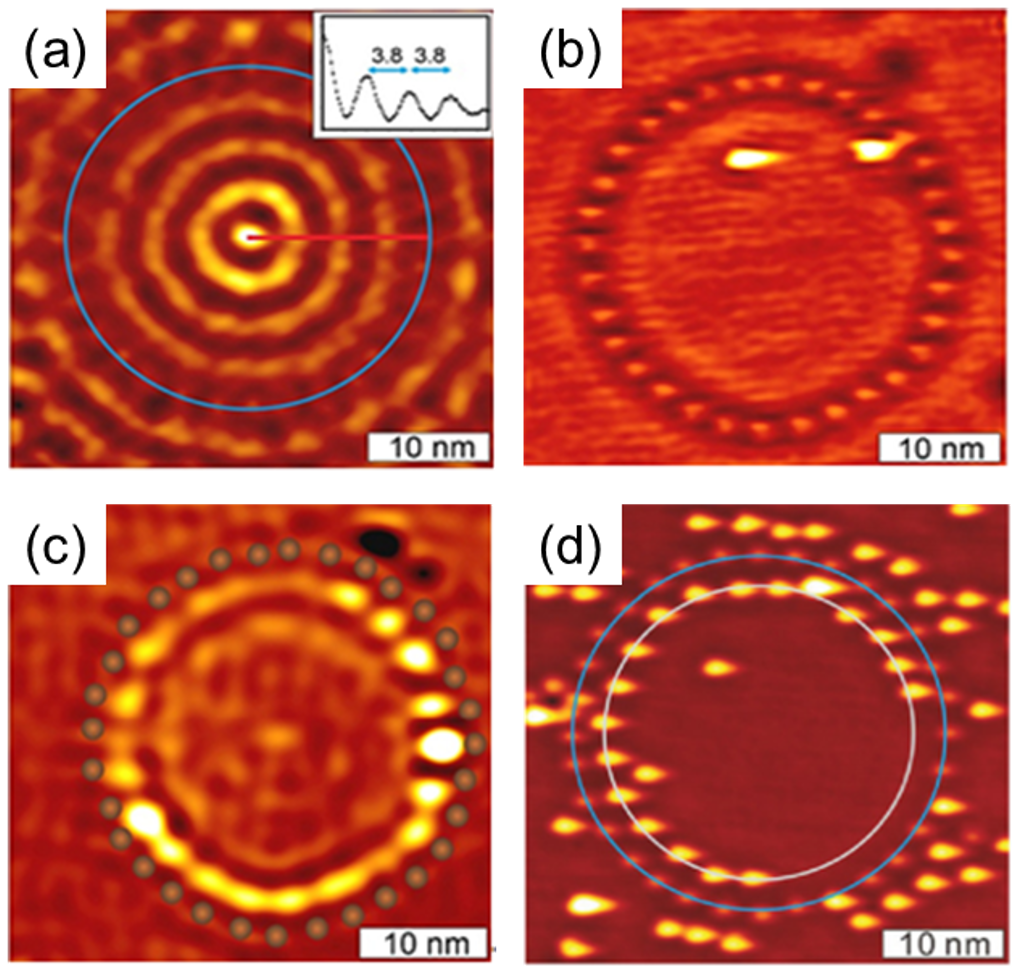
еӣҫ5. з”ЁйҮҸеӯҗеӣҙж Ҹз ”з©¶йҮҸеӯҗеҸ—йҷҗдёӢзҡ„еҺҹеӯҗжү©ж•Ј гҖӮ (a) еҚ•жҷ¶ Ag (111) дёҠз”ұ 32 дёӘ Fe еҺҹеӯҗжһ„е»әжҲҗзҡ„гҖҒзӣҙеҫ„дёә 30 nm зҡ„еңҶеҪўеӣҙж Ҹ гҖӮ еӣҙж ҸеҶ…йғЁзҡ„з”өеӯҗжң¬еҫҒжҖҒеҜҶеәҰжҢҜиҚЎеҲҶеёғ (еҚійҮҸеӯҗжіўеҠЁе№Іж¶үжүҖиҮҙзҡ„е№Іж¶үзҺҜ) жё…жҷ°еҸҜи§Ғ (и§ҒжҸ’еӣҫ) пјҢ е№Іж¶үзҺҜй—ҙи·қеӨ§зәҰ 3.8 nm пјҢ е№Іж¶үзҺҜжҢҜе№…з”ұдёӯеҝғеҗ‘еӨ–дёҚж–ӯеҮҸејұ гҖӮ (b) дёӨдёӘ Gd еҺҹеӯҗ (дёӨдёӘиҖҖж–‘зӮ№еҚідёәе…¶дҪҚзҪ®) йҖҡиҝҮз”өеӯҗжқҹи’ёеҸ‘жІүз§ҜеҲ°еӣҙж ҸеҶ… пјҢ зӣёи·қеӨ§зәҰ 7.0 nm гҖӮ 32 дёӘ Fe еҺҹеӯҗжһ„жҲҗзҡ„еӣҙж ҸиЎ¬еәҰжё…жҷ°еҸҜиҫЁ гҖӮ (c) еңЁдёҚеҗҢж—¶й—ҙеҶ…йҡҸжңәйҮҮйӣҶ 500 еӨҡе№…еӣҫеғҸ пјҢ 然еҗҺе°Ҷиҝҷ 500 е№…еӣҫеғҸеҸ еҠ иө·жқҘ пјҢ е°ұеҪўжҲҗдәҶиҝҷдёӨдёӘ Gd еҺҹеӯҗзҡ„дҪҚзҪ®жҰӮзҺҮеҲҶеёғеӣҫ гҖӮ иҝҷйҮҢ пјҢ дә®еәҰи¶Ҡй«ҳиЎЁзӨәжӯӨеӨ„ Gd еҚ жҚ®зҡ„жҰӮзҺҮи¶Ҡй«ҳ гҖӮ д»”з»ҶиҫЁи®Ө пјҢ еҸҜд»ҘзңӢеҲ° Gd еҺҹеӯҗеҲҶеёғе‘ҲзҺ°дёүдёӘеңҶзҺҜ пјҢ и¶Ҡйқ иҝ‘ Fe еҺҹеӯҗеӣҙж Ҹ пјҢ еңҶзҺҜдә®еәҰи¶Ҡй«ҳ гҖӮ и¶Ҡйқ иҝ‘дёӯеҝғзҡ„еңҶзҺҜиЎ¬еәҰи¶Ҡжҡ— пјҢ йҡҫд»ҘеҲҶиҫЁ гҖӮ (d) еңЁеӣҙж ҸеҶ…йғЁж”ҫзҪ® 20 дёӘ Gd еҺҹеӯҗ пјҢ дёҖж®өж—¶й—ҙеҗҺеҸҜд»ҘзңӢеҲ°иҝҷдәӣ Gd еҺҹеӯҗдјҡеңЁйқ иҝ‘еӣҙж ҸеҶ…жөӢеҪўжҲҗдёҖдёӘдёҚй—ӯеҗҲзҡ„еңҶзҺҜ (еӣҫдёӯз”Ёй«ҳдә®зҡ„з»Ҷзәҝе°ҶзҺҜиҝһиө·жқҘ пјҢ д»ҘдҫҝиҫЁи®ӨпјӣеӨ–дҫ§зҡ„и“қзәҝж ҮиҜҶзҡ„жҳҜ Fe еҺҹеӯҗеӣҙж Ҹ) гҖӮ з»“жһңжқҘиҮӘж–ҮзҢ® [Phys. Rev. B 87, 085415 (2013)] гҖӮ
жҺЁиҚҗйҳ…иҜ»
- дәәеӨ§йҷ„дёӯ|第37еұҠе…ЁеӣҪдёӯеӯҰз”ҹзү©зҗҶз«һиөӣеҢ—дә¬иөӣеҢәиҺ·еҘ–еҗҚеҚ•е…¬еёғ
- дјҠз“Ұе°”В·иҙҫеҹғеј—|вҖңзү©зҗҶеҮ д№ҺдёҚеҸҠж јзҡ„еҸ°зҗғйҖүжүӢвҖқпјҡдјҠз“Ұе°”В·иҙҫеҹғеј—
- иҺұеӣ е“Ҳеҫ·|вҖңеҰӮжһңеҶҚж—©еҮ е№ҙпјҢйңҚйҮ‘еә”иҜҘд№ҹиғҪеҫ—иҜәеҘ–вҖқ& 2020иҜәиҙқе°”зү©зҗҶеӯҰеҘ–
- е№ҝд№үзӣёеҜ№и®ә|2020е№ҙиҜәиҙқе°”зү©зҗҶеӯҰеҘ–жқғеЁҒи§ЈиҜ»пјҢдҪ жғізҹҘйҒ“зҡ„йғҪеңЁиҝҷйҮҢпјҒ
- GolevkaBao|е®Үе®ҷеӨ§зҲҶзӮёеҸҲжңүж–°еҸ‘зҺ°пјҹзү©зҗҶеӯҰ家и§ӮжөӢеҲ°е®Үе®ҷејҰж–°иҝ№иұЎпјҢдҪҶд»ҚйңҖиҜҒе®һ
- иҜәиҙқе°”зү©зҗҶеӯҰеҘ–|иҜәиҙқе°”зү©зҗҶеӯҰеҘ–е…¬еёғпјҒдёүдәәиҺ·еҘ–пјҢеҢ…жӢ¬дёҖеҗҚеҘіеӨ©ж–ҮеӯҰ家
- |еҫ·еӣҪ科еӯҰ家иҺ·иҜәиҙқе°”зү©зҗҶеӯҰеҘ– й»ҳе…Ӣе°”иЎЁзӨәзҘқиҙә
- иҜәиҙқе°”зү©зҗҶеӯҰеҘ–|еҲҡеҲҡпјҢ2020е№ҙиҜәиҙқе°”зү©зҗҶеӯҰеҘ–жҸӯжҷ“пјҒ
- зү©зҗҶ|2020зү©зҗҶиҜәеҘ–ж„ҸеӨ–еҘ–з»ҷй»‘жҙһпјҢ专家称早иҜҘеҫ—
- зү©зҗҶ|и§ЈиҜ»2020е№ҙиҜәиҙқе°”зү©зҗҶеҘ–пҪң他们жүҫеҲ°дәҶе®Үе®ҷдёӯжңҖеҘҮејӮзҡ„з§ҳеҜҶ











