зү©зҗҶ|еӣҡзҰҒдәҺзәізұіеӣҙж Ҹдёӯзҡ„йҮҸеӯҗ( дәҢ )
http://tutorials.crystalsolutions.eu/tutorial.html?td=metalstf=index
https://iopscience.iop.org/article/10.1088/0953-8984/20/30/304209
2. йҮҸеӯҗеӣҙж Ҹд№Ӣжәҗ
еҪ“然 пјҢ иҝҷж ·зҡ„и‘өиҠұеӣҙж ҸжҳҜзү©зҗҶ пјҢ жңүеҝ…иҰҒеңЁиҝҷйҮҢеҠ д»Ҙз®ҖеҚ•иҜҙжҳҺ гҖӮ дәӢе®һдёҠ пјҢ Google е’Ңз»ҙеҹәзҷҫ科дёӯеҜ№жӯӨжңүеҗ„з§Қз»ҶиҮҙжҲ–з®ҖжҙҒзҡ„жҸҸиҝ°зүҲжң¬ пјҢ еӨ§жҰӮзҡ„зү©зҗҶ(дёҚдёҘи°Ё пјҢ еӨ§иҮҙзү©зҗҶеӣҫеғҸ)еҸҜжҢүз…§дёӢиҝ°еҮ жқЎзҙўйӘҘпјҡ
(1) з«Ӣж–№дҪ“зі»иҙөйҮ‘еұһ CuгҖҒAgгҖҒAu зҡ„з”өеӯҗз»“жһ„жңүдёҖдёӘе…ұеҗҢзү№зӮ№пјҡе…¶ (111) иЎЁйқўеӯҳеңЁиЎЁйқўз”өеӯҗжҖҒ гҖӮ жүҖи°“иЎЁйқўз”өеӯҗжҖҒжҳҜжҢҮиҙ№зұійқўеӨ„зҡ„з”өеӯҗеҚіиҪҪжөҒеӯҗеҸӘиғҪеңЁиЎЁйқўиҝҗеҠЁ пјҢ еҚіжүҖи°“иЎЁйқўдәҢз»ҙз”өеӯҗж°” пјҢ иЎЁйқўеұӮз”өеӯҗж— жі•еҗ‘ж·ұеәҰж–№еҗ‘дј иҫ“ гҖӮ иҝҷдёҖж•Ҳеә”дёҺжҲ‘们йҖҡеёёзҗҶи§Јзҡ„йҮ‘еұһеҜјз”өзҺ°иұЎдёҚдёҖиҮҙпјҡиҝҷжҳҜйҮ‘еұһе•Ҡ пјҢ жҖҺд№ҲдјҡжІҝжҹҗдәӣж–№еҗ‘иҝҳдёҚиғҪеҜјз”өдәҶпјҹеІӮжңүжӯӨзҗҶпјҒ
(2) д»ҘйҮ‘еұһ Cu дёәдҫӢ пјҢ иЎЁйқўжҖҒзҡ„еҪўжҲҗжңәеҲ¶еӨ§зәҰжҳҜпјҡеҸӮиҖғеӣҫ 2(a) жүҖзӨәзҡ„йҮ‘еұһ Cu иғҪеёҰз»“жһ„ пјҢ еҸҜи§ҒеҫҲеӨҡиғҪеёҰз©ҝи¶Ҡиҙ№зұійқў пјҢ дҪҝеҫ— Cu жҲҗдёәйҮ‘еұһ гҖӮ дёҚиҝҮ пјҢ еҰӮжһңд»”з»ҶеҺ»зңӢеҠЁйҮҸз©әй—ҙеёғйҮҢжёҠеҢәзҡ„ О“ вҖ“ L зәҝж®өеҚідёәе®һз©әй—ҙзҡ„ [111] ж–№еҗ‘ пјҢ иҝҷдёӘеҢәеҹҹжІЎжңүд»»дҪ•иғҪеёҰз©ҝи¶Ҡ пјҢ ж„Ҹе‘ізқҖжІҝиҝҷдёӘж–№еҗ‘жңүиғҪйҡҷгҖҒжҳҜзҰҒеёҰ пјҢ з”өеӯҗж— жі•жІҝжӯӨж–№еҗ‘иҝҗеҠЁ гҖӮ жӣҙдёәжё…жҷ°зҡ„иЎЁиҫҫеңЁеӣҫ 2(b) жүҖзӨәд№Ӣ Cu (111) йқўиҙ№зұійқўйҷ„иҝ‘зҡ„иүІж•Је…ізі» гҖӮ еҸҜи§Ғиҙ№зұійқўеӨ„зҡ„жіўзҹў kF иүІж•ЈдёҚйҖҡиҝҮеқҗж ҮеҺҹзӮ№ [0, 0] пјҢ иҖҢиҝҷдёҖзӮ№жӯЈд»ЈиЎЁ [111] ж–№еҗ‘ гҖӮ д№ҹе°ұжҳҜиҜҙ пјҢ еҺҹзӮ№ [0, 0] еӨ„зҡ„жҖҒеҜҶеәҰдёәйӣ¶пјҡз»қзјҳпјҒ
(3) еҪ“然 пјҢ Cu (111) иЎЁйқўзҡ„з”өеӯҗд№ҹдёҚиғҪи„ұзҰ»иЎЁйқўи·‘еҲ°зңҹз©әжҲ–иҖ…з©әж°”дёӯ гҖӮ еӣ дёәеҠҹеҮҪж•°зҡ„жқҹзјҡ пјҢ з”өеӯҗдёҚиғҪйҖёе…Ҙзңҹз©ә гҖӮ еӣ жӯӨ пјҢ Cu (111) иЎЁйқўзҡ„з”өеӯҗе®һйҷ…дёҠе°ұжҳҜдёҖеұӮе№іиЎҢдәҺиЎЁйқўиҝҗеҠЁзҡ„дәҢз»ҙз”өеӯҗж°” пјҢ зұ»дјјдәҺи°ғеҲ¶жҺәжқӮзҡ„з•Ңйқў гҖӮ
(4) иҝҷдәӣз”өеӯҗж°”зҡ„иҝҗеҠЁдјҡеҸ—еҲ°иЎЁйқўеҸ°йҳ¶гҖҒеҗёйҷ„еҺҹеӯҗзӯүеҗ„з§ҚдёҚе®Ңж•ҙз»“жһ„зҡ„ж•Је°„еҪұе“Қ пјҢ иЎЁзҺ°дёәз”ұдәҺиЎЁйқўдәҢз»ҙдёҘж је‘ЁжңҹжҖ§еҠҝеңәиў«з ҙеқҸиҖҢдҪҝз”өеӯҗжіўеҠЁеҸ—еҲ°ж•Је°„ пјҢ дјҡеҪўжҲҗеҗ„з§ҚжіўеҠЁиҠұж · гҖӮ
(5) Crommie зӯүеҸ‘зҺ°зҡ„ Cu (111) д№ӢйҮҸеӯҗеӣҙж ҸиҠұж · пјҢ е®һиҙЁдёҠеҚіеӣҙж ҸеҶ…йғЁзҡ„з”өеӯҗиҝҗеҠЁиў«еӣҙж ҸеҸҚе°„еӣһеҺ» пјҢ дёҺеҗҺз»ӯиҝҗеҠЁиҖҢжқҘзҡ„з”өеӯҗеҪўжҲҗе№Іж¶ү гҖӮ иҖғиҷ‘еҲ°з”өеӯҗжіўеҠЁзҡ„жң¬иҙЁ пјҢ жғіиұЎдёҖдёӢж°ҙеЎҳд№Ӣж°ҙжіўж¶ҹжјӘ пјҢ еӣҫ 1(a) жүҖзӨәзҡ„е№Іж¶үиҠұж ·еҫҲе®№жҳ“е®ҡжҖ§зҗҶи§Ј гҖӮ дҪҚдәҺеӣҙж Ҹдёӯеҝғзҡ„вҖңзҒ«зӮ¬вҖқд№ҹжҳҜе№Іж¶үзҡ„з»“жһң гҖӮ
(6) иЎЁйқўдёҠйӮЈдәӣеҚ•дёӘ Fe еҺҹеӯҗе‘Ёеӣҙд№ҹжңүзұ»дјјзү©зҗҶиҝҮзЁӢпјҡе…Ҙе°„зҡ„иЎЁйқўжҖҒз”өеӯҗжіўдёҺиў« Fe еҺҹеӯҗж•Је°„зҡ„з”өеӯҗжіўд№Ӣй—ҙе№Іж¶ү пјҢ еҪўжҲҗеӣҙз»• Fe еҺҹеӯҗзҡ„й©»жіў пјҢ еҚіеҰӮеӣҫ 1(a) дёӯзәўиүІз®ӯеӨҙжүҖжҢҮ гҖӮ
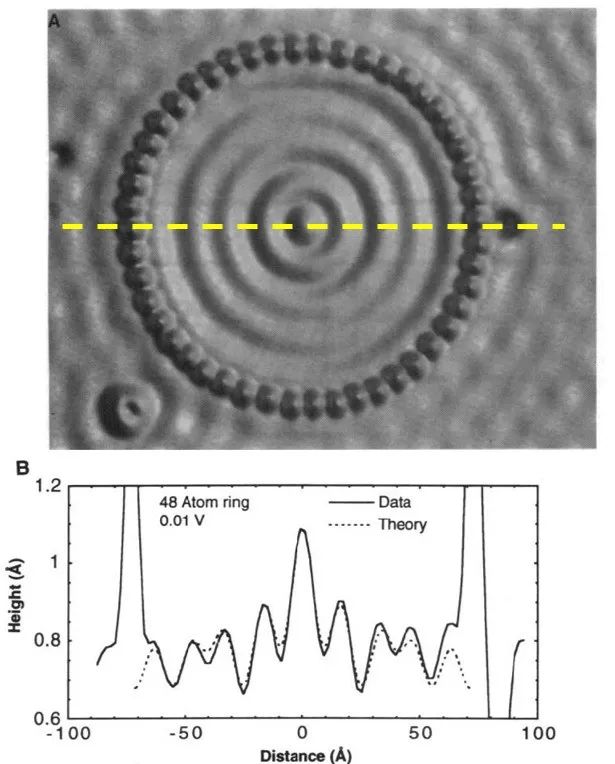
笔иҖ…ж„ҝж„ҸиҜҙ пјҢ зү©зҗҶеҒҡеҲ°иҝҷдёӘд»ҪдёҠ пјҢ ж„ҹи§үзү©зҗҶдәәе°ұжҳҜеңЁеҮӯе…ҙиҮҙзҺ©жёёжҲҸ гҖӮ е…ҙи¶ЈжүҖиҮҙ пјҢ дёҚдәҰд№җд№ҺпјҒеҪ“然 пјҢ еӣҫ 1 жүҖзӨәзҡ„еӣҫж ·жҳҜз»ҸиҝҮеҗҺжңҹд»”з»Ҷдҝ®йҘ°е’ҢиүәжңҜеҢ–еӨ„зҗҶиҝҮ пјҢ еӣ жӯӨжҲҗдёәзҸҚе“Ғ гҖӮ дёҖејҖе§ӢеҸ‘иЎЁеңЁ Science жңҹеҲҠдёҠзҡ„еӣҫеғҸеҰӮеӣҫ 3 жүҖзӨә пјҢ жҳҫеҫ—з®ҖйҷӢиҖҢжҡ—ж·Ў пјҢ иҷҪ然зү©зҗҶжҲҗеҲҶдёҖзӮ№д№ҹдёҚзјә гҖӮ еҰӮжһңжІҝеӣҫ 2 дёҠйғЁеӣҫеғҸзҡ„й»„иүІиҷҡзәҝиҝӣиЎҢ profile зәҝжү«жҸҸ пјҢ еҚіеҫ—еҲ°еӣҫ 2 дёӢйғЁзҡ„й«ҳеәҰеҲҶеёғжӣІзәҝ пјҢ иЎЁиҫҫдәҶжң¬еҫҒжҖҒеҜҶеәҰзҡ„еҲҶеёғ гҖӮ еҸҜд»ҘзңӢеҲ° пјҢ иҝҷз§ҚжіўеҠЁе№Іж¶үж•Ҳеә”дёҚжҳҜдёӘе°ҸдҝЎеҸ· пјҢ иҝҳжҳҜйқһеёёжҳҫи‘—зҡ„ гҖӮ
жң¬ж–ҮеӣҫзүҮ
еӣҫ3. йҮҸеӯҗеӣҙж Ҹжң¬еҫҒжҖҒзҡ„з©әй—ҙеӣҫеғҸ гҖӮ дёҠеӣҫ A зҡ„йҮҸеӯҗеӣҙж ҸиҠұж ·еҚіеӣҫ 1(a) пјҢ е…¶дёӯй»„иүІиҷҡзәҝдёә笔иҖ…ж·»еҠ пјҢ жІҝиҝҷдёҖиҷҡзәҝзәҝжү«жҸҸ пјҢ еҫ—еҲ°зҡ„жҖҒеҜҶеәҰеҲҶеёғеӣҫеҰӮдёӢеӣҫ B жүҖзӨә гҖӮ еҸҜд»ҘзңӢеҲ° пјҢ еӣҙж ҸдёӯеҝғеҺҹзӮ№еӨ„ (еҚізҒ«зӮ¬еӨ„) жҖҒеҜҶеәҰжңҖй«ҳ пјҢ 然еҗҺжІҝеҚҠеҫ„еҗ‘еӨ–еҪўжҲҗжҖҒеҜҶеәҰжҢҜиҚЎ пјҢ дҪҶжҢҜе№…и¶ҠжқҘи¶Ҡе°Ҹ пјҢ жҳҫзӨәжіўеҠЁе№Іж¶үж•Ҳеә”еҸҳејұ пјҢ жҖҒеҜҶеәҰеҸҳдҪҺ гҖӮ From M. F. Crommie, C. P. Lutz, and D. M. Eigler, Science 262, 218 (1993).
3. йҮҸеӯҗе°әеҜёж•Ҳеә”
иҮіжӯӨ пјҢ 笔иҖ…е·®дёҚеӨҡзӮ«иҖҖе®ҢеӨ§зәҰдёүеҚҒе№ҙеүҚзү©зҗҶеӯҰзҡ„дёҖйЎ№жҲҗжһңвҖ”вҖ”йҮҸеӯҗеӣҙж ҸеҸҠе…¶еҜ№еұҖеҹҹз”өеӯҗжҖҒеҜҶеәҰзҡ„и°ғжҺ§ гҖӮ иҝҷйЎ№ејҖеҲӣжҖ§зҡ„е·ҘдҪңејҖеҗҜдәҶеҲ©з”ЁйҮҸеӯҗеӣҙж Ҹз ”з©¶йҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„еӨ§й—Ё гҖӮ
жүҖи°“йҮҸеӯҗе°әеҜёж•Ҳеә” пјҢ жҳҜйҮҸеӯҗдё–з•ҢжңҖеҹәжң¬зҡ„ж•Ҳеә”д№ӢдёҖ гҖӮ е®ғжҸҸиҝ°зҡ„жҳҜиҝҷж ·дёҖз§ҚзҺ°иұЎпјҡеҪ“и§ӮжөӢеҜ№иұЎзҡ„е°әеҜёеӨ§е°Ҹе’ҢиҪҪжөҒеӯҗжңүж•Ҳеҫ·еёғзҪ—ж„Ҹжіўй•ҝеҸҜзӣёжҜ”жӢҹж—¶ пјҢ ж №жҚ®йҮҸеӯҗеҠӣеӯҰ пјҢ иҝҷз§Қжғ…еҶөдёӢиҪҪжөҒеӯҗиғҪйҮҸдјҡеҮәзҺ°жҳҺжҳҫзҡ„йҮҸеӯҗеҢ–зҺ°иұЎ пјҢ дёҖзі»еҲ—йҮҸеӯҗеҢ–зҡ„зү©зҗҶжҖ§иҙЁеҚіиЎЁзҺ°еҮәжқҘ гҖӮ йҷӨдәҶ科еӯҰжң¬иә«зҡ„ж„Ҹд№үд№ӢеӨ– пјҢ йҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„еә”з”ЁиғҢжҷҜд№ғдёҺдј з»ҹзЎ…еҹәеҷЁд»¶еңЁи¶…е°ҸеһӢеҢ–иҝҮзЁӢдёӯйҖҗжёҗи¶Ӣиҝ‘ж ҮеәҰжһҒйҷҗжңүе…і гҖӮ йҡҸзқҖеҷЁд»¶еҗ‘ж ҮеәҰжһҒйҷҗи¶Ӣиҝ‘ пјҢ йҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„йҮҚиҰҒжҖ§дёҺж—Ҙдҝұеўһ пјҢ жҺўзҙўжӯӨж•Ҳеә”дәҰиғҪеӨҹдёәдҝЎжҒҜеӨ„зҗҶе’Ңи®Ўз®—жҸҗдҫӣйўқеӨ–зҡ„еҸҜиғҪжҖ§е’ҢеҸҜдҫӣйҖүжӢ©зҡ„жһ„жһ¶ гҖӮ
еҫҲжҳҫ然 пјҢ з ”з©¶йҮҸеӯҗе°әеҜёж•Ҳеә”жңҖз®ҖеҚ•зҡ„еҠһжі•еҚіе°Ҷз ”з©¶еҜ№иұЎеҒҡеҲ°еҫҲе°Ҹ пјҢ 然еҗҺиҜ„дј°жҖ§иғҪдёҺе°әеҜёд№Ӣй—ҙзҡ„е…ізі» пјҢ зңӢзңӢе…¶еҰӮдҪ•еҒҸзҰ»дј з»ҹзү©зҗҶжңәеҲ¶ гҖӮ дёҚиҝҮ пјҢ иҝҷж ·зҡ„з ”з©¶зәҜзІ№жҳҜз»ҸйӘҢе’Ңй—ҙжҺҘзҡ„ пјҢ ж— жі•зӣҙжҺҘе’Ңе®ҡйҮҸдҪ“зҺ°йҮҸеӯҗе°әеҜёж•Ҳеә”еҲ°еә•е‘ҲзҺ°д»Җд№Ҳж—¶з©әзү№еҫҒ гҖӮ еҮәи·ҜеңЁе“ӘйҮҢе‘ўпјҹиҷҪ然з»ҸиҝҮж—Ҙз§ҜжңҲзҙҜ пјҢ жҺўжөӢйҮҸеӯҗе°әеҜёж•Ҳеә”зҡ„жүӢж®өе’Ңж–№жі•е·Із»ҸжңүеҫҲеӨҡ пјҢ дҪҶ STM зңӢиө·жқҘжӯЈеңЁжҲҗдёәжңҖеҗҲйҖӮзҡ„жүӢж®өд№ӢдёҖпјҡSTM жү«жҸҸйҡ§йҒ“жҳҫеҫ®жңҜдёҚд»…еҸҜиҺ·еҫ—ж ·е“ҒиЎЁйқў (йҖҡеёёжҳҜйҮ‘еұһе’ҢеҚҠеҜјдҪ“) еҺҹеӯҗзә§еҲ«зҡ„еҪўиІҢ пјҢ иҝҳеҸҜд»ҘжҸҗеҸ–е®ғзҡ„еұҖеҹҹжҖҒеҜҶеәҰзҡ„ж—¶з©әдҝЎжҒҜ гҖӮ йҷӨжӯӨд№ӢеӨ– пјҢ STM зҡ„еҸҰеӨ–дёҖдёӘзӢ¬е…·зү№иүІзҡ„еҠҹиғҪвҖ”вҖ”еңЁж ·е“ҒиЎЁйқўиҝӣиЎҢеҺҹеӯҗж“ҚзәөвҖ”вҖ”дҪҝеҫ—дәә们еҸҜд»ҘеңЁж ·е“ҒиЎЁйқўж“ҚзәөеҺҹеӯҗжқҘиҮӘз”ұең°жһ„йҖ жҹҗдәӣз»“жһ„ пјҢ е®ҡйҮҸз ”з©¶йҮҸеӯҗж•Ҳеә” гҖӮ
жҺЁиҚҗйҳ…иҜ»
- дәәеӨ§йҷ„дёӯ|第37еұҠе…ЁеӣҪдёӯеӯҰз”ҹзү©зҗҶз«һиөӣеҢ—дә¬иөӣеҢәиҺ·еҘ–еҗҚеҚ•е…¬еёғ
- дјҠз“Ұе°”В·иҙҫеҹғеј—|вҖңзү©зҗҶеҮ д№ҺдёҚеҸҠж јзҡ„еҸ°зҗғйҖүжүӢвҖқпјҡдјҠз“Ұе°”В·иҙҫеҹғеј—
- иҺұеӣ е“Ҳеҫ·|вҖңеҰӮжһңеҶҚж—©еҮ е№ҙпјҢйңҚйҮ‘еә”иҜҘд№ҹиғҪеҫ—иҜәеҘ–вҖқ& 2020иҜәиҙқе°”зү©зҗҶеӯҰеҘ–
- е№ҝд№үзӣёеҜ№и®ә|2020е№ҙиҜәиҙқе°”зү©зҗҶеӯҰеҘ–жқғеЁҒи§ЈиҜ»пјҢдҪ жғізҹҘйҒ“зҡ„йғҪеңЁиҝҷйҮҢпјҒ
- GolevkaBao|е®Үе®ҷеӨ§зҲҶзӮёеҸҲжңүж–°еҸ‘зҺ°пјҹзү©зҗҶеӯҰ家и§ӮжөӢеҲ°е®Үе®ҷејҰж–°иҝ№иұЎпјҢдҪҶд»ҚйңҖиҜҒе®һ
- иҜәиҙқе°”зү©зҗҶеӯҰеҘ–|иҜәиҙқе°”зү©зҗҶеӯҰеҘ–е…¬еёғпјҒдёүдәәиҺ·еҘ–пјҢеҢ…жӢ¬дёҖеҗҚеҘіеӨ©ж–ҮеӯҰ家
- |еҫ·еӣҪ科еӯҰ家иҺ·иҜәиҙқе°”зү©зҗҶеӯҰеҘ– й»ҳе…Ӣе°”иЎЁзӨәзҘқиҙә
- иҜәиҙқе°”зү©зҗҶеӯҰеҘ–|еҲҡеҲҡпјҢ2020е№ҙиҜәиҙқе°”зү©зҗҶеӯҰеҘ–жҸӯжҷ“пјҒ
- зү©зҗҶ|2020зү©зҗҶиҜәеҘ–ж„ҸеӨ–еҘ–з»ҷй»‘жҙһпјҢ专家称早иҜҘеҫ—
- зү©зҗҶ|и§ЈиҜ»2020е№ҙиҜәиҙқе°”зү©зҗҶеҘ–пҪң他们жүҫеҲ°дәҶе®Үе®ҷдёӯжңҖеҘҮејӮзҡ„з§ҳеҜҶ











