江苏龙网

  1. 首页 > 资讯 > 资讯 > >

|想要看懂《信条》，演反间时懂先得你

这几天 ， 小编的朋友圈和各类社交平台都被一部“爆炒脑花”影片的观后感刷屏
“看了一天的分析解说依然懵逼的我选择放弃 ， 算了是我不配”
“情节让我怀疑自己是不是学物理的”
“开心地进去 ， 懵逼地出来”
“看了个寂寞”
这些评论让买好票但还没去看的小编感到一丝丝恐慌
|想要看懂《信条》，演反间时懂先得你
本文图片

为了不在同去看电影的朋友面前露怯 ， 小编求助一位从电影院出来、刚刚失去脑花的同学 ， 希望他能在不剧透的前提下为我讲解疑难知识点 。
然后他露出蜜汁笑容：“剧透也没关系的 ， 反正你第一遍肯定看不懂 。 ”
|想要看懂《信条》，演反间时懂先得你
本文图片

真的吗？真的有这么烧脑吗？
受到惊吓的小编忐忑地走进电影院 ， 经历了两个半小时的头脑风暴之后 ， 对比满脸问号的友人 ， 作为一个日常和时间反演打交道的专（wu）业（li）人（cai）士（ji） ， 小编露出了自信的微笑 。 为了让大家不仅去感受 ， 更要试图理解这部电影 ， 小编决定效仿片中的科学家 ， 从热力学第二定律开始说起 。
|想要看懂《信条》，演反间时懂先得你
本文图片

01
热力学第二定律
热力学第二定律有许多不同的表述 ， 比如最经典的开尔文表述和克劳修斯表述 。
开尔文表述
不可能从单一热源吸热使之完全变为有用的功而不产生其他影响
克劳修斯表述
不可能把热从低温物体传到高温物体而不产生其他影响
除此之外还有普朗克表述和喀喇西奥多里表述等等 ， 但不论表述形式如何 ， 它们的本质都是相同的：揭示自然界中所存在的不可逆过程 。 例如开尔文表述所要表达的就是“热”和“功”之间转化的不可逆性：在不产生其他影响的情况下 ， 功可以完全转化成热 ， 但是热不能完全转化成功 。 而克劳修斯则更为直接地表述了不可逆过程（热传导）中的方向性 。 对方向性的理解是：它不仅不能反向重演正向过程 ， 也无法完全恢复原状而不留下任何影响 。 举个通俗易懂的例子 ， 回家后 ， 你的房间在几天之内变得杂乱无章就是个不可逆过程 ， 不会有家养小精灵听见你的祈求帮你把房间整理干净 ， 如果想恢复原状 ， 要么自己动手整理 ， 要么被妈妈骂一顿后动手整理（雾
概括来说 ， 热力学第一定律告诉我们热现象过程必须满足能量守恒 ， 热力学第二定律则指明了这些热现象过程是具有方向性的不可逆过程 。
为了判断某一过程是否可逆 ， 以及为不可逆过程的方向提供判断的标准 ， “天选之子”——态函数熵诞生了 。
02
"熵"的提出
“熵”的概念要追溯到几个世纪以前 ， 那时人们发现燃烧反应所放出的能量中总有一部分由于耗散和损失、无法转化为有用功 。 早期由英国人萨维利、纽可门分别于1698年和1712年各自独立发明的蒸汽机 ， 以及1769年法国人居纽制造的世界上第一辆蒸汽驱动三轮汽车效率都很低下 ， 只能将不到2%的输入能量转化为有用功输出 。 在后来的两个世纪中 ， 物理学家一直在研究能量损失的原因 。 在1850年代初期 ， 鲁道夫·克劳修斯提出了热力学系统的概念 ， 发展了关于能量损失的理论 ， 并在提出了热力学第二定律后不久 ， 首次从宏观上提出了"熵"(Entropy)的概念 。
【|想要看懂《信条》，演反间时懂先得你】克劳修斯的“熵”是从经典热力学的角度定义的 ， 此时不考虑处于热力学平衡态的体系的微观细节 ， 熵是描述整个体系的态函数 ， 由一些状态变量（几何变量：体积、表面积、长度；力学变量：压强、表面张力等；电磁变量：电场强度、磁场强度等；化学变量：组元的摩尔数）确定 。 我们现在可以跟着克劳修斯的足迹 ， 从卡诺定理出发引入态函数“熵” 。
卡诺定理
所有工作于两个一定温度之间的热机的效率 ， 不能大于工作于同样两个温度之间的可逆卡诺热机的效率
即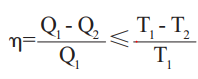
|想要看懂《信条》，演反间时懂先得你
本文图片

Q1是热机从温度为T1的高温热源吸收的热量 ， Q2是热机向温度为T2的热源放出的热量 ， η是热机的效率 。 其中=适用于可逆热机 ， ≠适用于不可逆热机 。 如果把传递给热机的热量规定为正 ， 热机放出的热量规定为负 ， 上式可以写成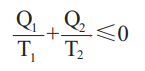
|想要看懂《信条》，演反间时懂先得你
本文图片

将这个式子推广 ， 可以得到克劳修斯不等式
由可逆过程环路积分为零 ， 我们可以定义一个态函数的全分量dQ/T=dS ， 这个态函数S就是熵 ， 结合不可逆过程我们易得


推荐阅读


上一篇：天文|我们似乎总是更爱假设外星人拥有比我们更加先进的科技

下一篇：暖心 大学|“暖心公主抱”女生考上大学 拿着录取通知书与民警分享喜悦