江苏龙网

  1. 首页 > 资讯 > 资讯 > >

量子计算机|到底什么是量子计算( 四 )


有没有一种量子纠错码 ， 它的宇称查验和重复码类似 ， 只是对近邻量子比特的测量？由于在物理系统中量子比特之间往往是近邻相互作用 ， 这样的纠错码更容易实现 。 1997 年 ， 凯达耶夫(A.Kitaev)提出了拓扑码[19] ， 根据边界条件的不同 ， 也被称为环面码或表面码(图3) 。 此后又发现了其他具有类似性质的量子纠错码 。 对于量子计算来说 ， 目前综合看来表面码可能是纠错码最好的选择 。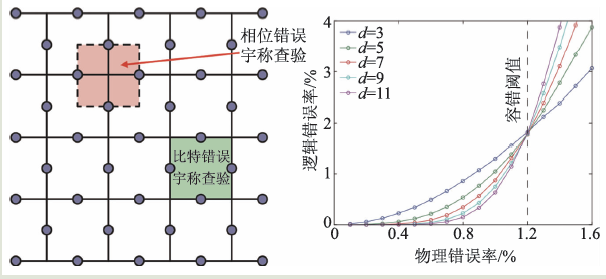
量子计算机|到底什么是量子计算
本文图片

图3 表面码和容错阈值
4.2 容错阈值
在量子计算中 ， 需要通过对物理量子比特的操作来实现量子纠错所需要的宇称查验 。 而每一次操作都有一定概率引入错误 ， 有可能导致纠错本身起到负面作用 。 因此 ， 如果量子纠错能够起到预期效果 ， 其前提条件是宇称查验过程中产生的错误不会使得错误没有减少反而增加了 。 这个条件被量化为容错阈值：当单次操作的错误率小于阈值的时候 ， 量子纠错才能起到应有的作用 。
对于表面码来说 ， 当物理量子比特单次操作的错误率低于阈值的时候 ， 纠错后逻辑量子比特的错误率随着表面码尺寸(码距)的增加而降低 ， 如图3 所示 。 事实上 ， 这种情况下逻辑错误率随着码距指数衰减 。 因此 ， 我们可以通过增加码距 ， 也就是使用更多的物理量子比特 ， 来降低逻辑错误率 。 只要物理量子比特足够多 ， 逻辑错误率就会足够低 。 数值模拟表明表面码的错误率阈值大约是1%[20] 。
 关于容错阈值的两点说明·
(1)阈值一般是在对错误分布的合理假设下得到的 ， 假设与真实的物理系统之间还存在着差异 。 一般来说 ， 假设包括每次操作的错误是独立分布的 。 常用的模型是去极化模型 ， 即当错误发生的时候 ， 相应物理量子比特的量子态完全被破坏 。
(2)阈值是对单次操作的错误率来说的 。 例如整个计算包括N次操作 ， 每次操作的错误率为p ， 那么在物理量子比特上发生错误的个数大概是Np 。 即使在Np1 的情况下 ， 只要p 小于阈值并且量子纠错码足够大 ， 逻辑量子比特出错的概率还是可以足够低 。
4.3 容错量子计算
通过查验物理量子比特之间的关系 ， 逻辑量子比特被保护起来了 。 除此以外 ， 我们还需要对逻辑量子比特进行操作来实现通用量子计算 。 并且这些操作不应该破坏对逻辑量子比特的保护 。 在这方面已经有大量的研究 。 为了能够进行通用量子计算 ， 需要一组逻辑量子比特操作 ， 包括初始化、通用量子门以及读取 。 其中某些操作可以直接进行而不明显增加逻辑错误率 ， 另外一些操作需要通过引入魔术态[21]等处理方法来进行 。 容错量子计算的过程如图4 所示 ， 这里不再赘述 。 总的来说 ， 理论上基于逻辑量子比特的通用量子计算是可行的 。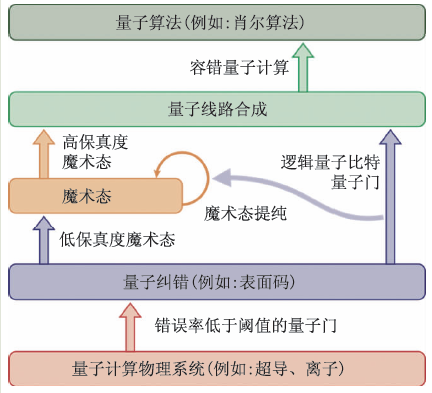
量子计算机|到底什么是量子计算
本文图片

图4 容错量子计算
目前看来 ， 表面码可能是实现容错量子计算最好的选择 。 首先 ， 表面码具有较高的容错阈值(～1%) 。 其次 ， 表面码仅需要在近邻量子比特之间进行宇称查验 ， 容易在物理系统中实现 。 虽然通过CSS码的级联可以得到更高的阈值(～3%)[22] ， 但需要在远距离量子比特之间进行宇称查验 ， 也就是需要量子计算机内部的高保真度量子态传输 ， 因此在物理系统中实现的难度更高 。
实现容错量子计算需要一台拥有大量低错误率量子比特的量子计算机 。 在亚阈值的条件下 ， 只要物理量子比特数量足够多 ， 码距足够大 ， 我们就能够运行任意复杂的量子算法 。 需要的量子比特数量由错误率以及算法决定 。 对于表面码 ， 操作逻辑量子比特的错误率可以用P～d(100p)(d+1)/2来粗略估计 ， 其中p 是物理错误率 ， d 是码距[23] 。 一个逻辑量子比特需要的物理量子比特数量大约为(2d－1)2 。 如果我们考虑利用肖尔算法分解RSA系统中1000 位的二进制整数 ， 逻辑操作的数量大约在1011的数量级 ， 因此逻辑错误率P 需要达到10-12的水平 。 我们还假设需要1000 个逻辑量子比特用于存储整数 ， 并需要大约10 倍的量子比特用于辅助 ， 包括魔术态制备等 。 这样就能估计所需要物理量子比特的总数 。 这里仅做最简单粗略的估计 ， 结果如图5所示 。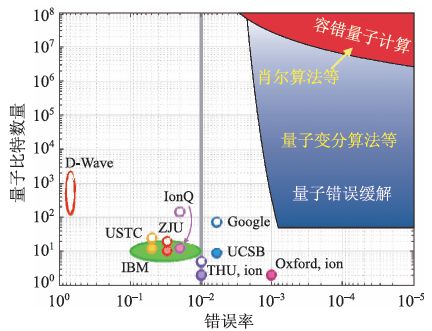
量子计算机|到底什么是量子计算
本文图片

图5 量子计算系统参数 。 灰线对应错误率p=1% ， 为表面码的阈值 。 D-Wave 系统为模拟量子计算机 ， 没有两量子比特门错误率 。 空心代表没有找到报道两量子比特门错误率测量实验结果的文献 。 作者注意到关于USTC量子门错误率的文献中提到 ， 利用随机校准测量的其系统中单个两量子比特门的错误率一般低于1%[30]
我们可以发现 ， 实现容错量子计算需要错误率明显低于阈值(到0.1%附近及以下)以及百万以上的物理量子比特 。 这对于目前的技术来说还是无法实现的 。


推荐阅读


上一篇：中央气象台：今年第9号台风“美莎克”昨日生成

下一篇：上海有3例确诊病例今日出院，共计829例治愈出院