宜宾学院|一道世界数学团体锦标赛真题,题目看似很难,其实很简单

文章图片
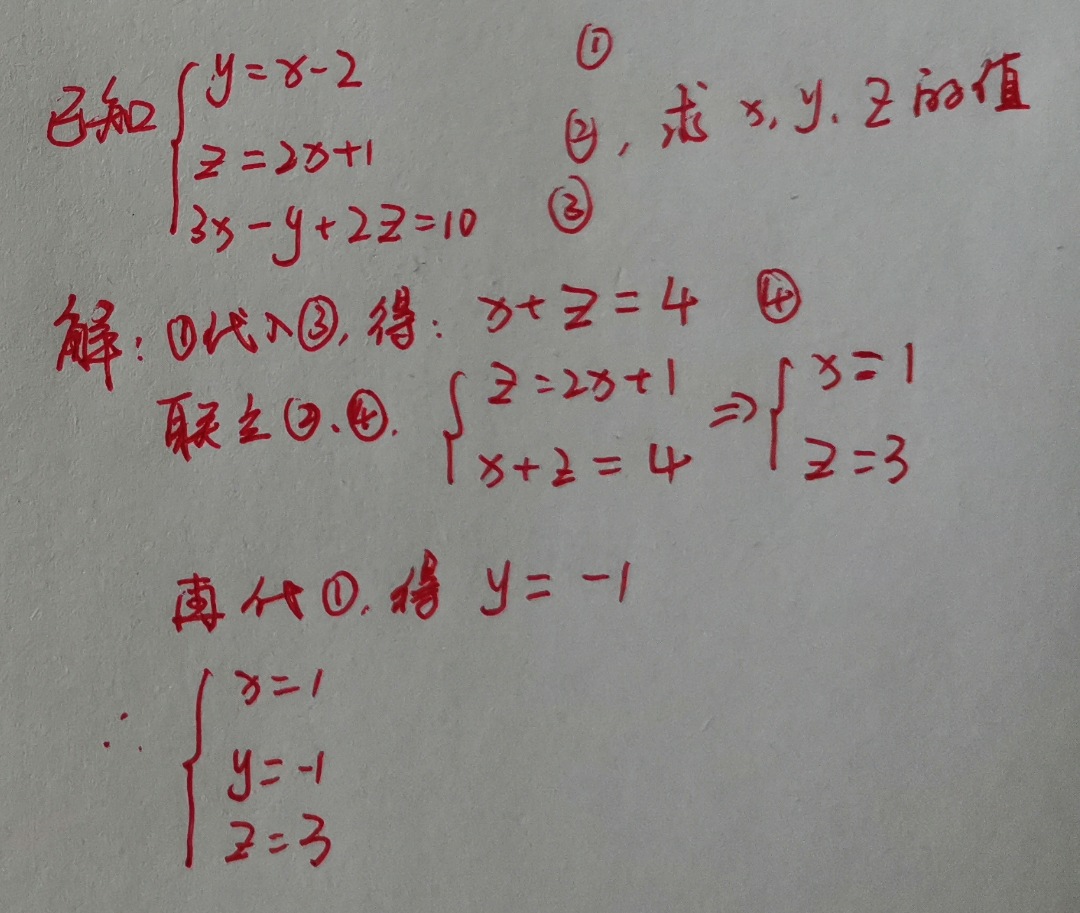
文章图片

文章图片

大家好 , 今天和大家分享一道世界数学团体锦标赛的题目:题干是一个多元方程组 , 然后求所给式子的值 。 只看题目 , 不少人都觉得挺难 , 但是仔细思考后不少初中生表示 , 这题也太简单了吧 。 下面我们一起来看一下这道题 。
如果只看题目 , 确实挺吓人的 。 已知条件是一个九元一次方程组 , 多元方程组的一般解题思路是:消元 , 将多元方程组变为一元方程 , 然后再分别求解 。 比如我们先看一个二元一次方程组的例子 。
消元的方法可以用代入法 , 也可以用加减消元法 , 可以根据题目和个人做题习惯自由选择 。 下面再来看一个三元一次方程组的例子 。
上面是两个简单的多元方程组的例子 。 其实 , 在解多元方程组时 , 除了某些特殊情况 , 一般来说有几个未知数就需要几个方程 。 从上面的例子也可以看出 , 二元一次方程组有2个方程 , 三元一次方程组有3个方程 。
再回到竞赛题 , 已知条件有A、B、C、D、E、F、G、H、I共9个未知数 , 如果要都求解出来 , 那么需要9个方程 , 但是已知条件只有7个方程 , 显然是不可能先把每个未知数都求出来的 。 那么究竟应该怎么求解呢?
我们先来观察一下所求式子的特点 , 然后尝试用整体代入的方法求解 。 这个方法可行不呢?显然是可行的 , 因为如果我们把A+E+I作为一个整体 , 那么这个方程组就只有7个未知数了 , 刚好可以求解出来 。 所以关键看就是看如何将A+E+I表示出来了 。
再仔细观察一下这个方程组 , A只在①式中出现 , I只在⑦式中出现 , 也就是表示这两个方程肯定需要用到 。 再看E , 在③、④、⑤三个方程中都出现了 , 那么究竟应该用哪个方程呢?仔细观察可以发现 , 如果用④式 , 刚好可以出现B+C+D和F+G+H的形式 。 这样就可以解出A+E+I的值 。
下面我们再来看另外一种解法 。
已知条件有9个未知数 , 但是只有7个方程 , 要想直接解出这9个未知数是不可能的 。 不过我们可以换一个方向来思考 , 那就是我们假设知道其中的某两个未知数的值 , 也是采用赋值法 , 然后可以将另外7个未知数全部解出来 , 再代入所求式子即可 。
用特殊值法求解 , 有人认为不够严谨 , 那么还有没有其他方法呢?当然有 。
虽然方程数少于未知数的个数 , 不能求出每个未知数的具体值 , 但是肯定可以找出他们之间的关系 。 比如我们可以把A、B当成已知量 , 然后用A、B把E和I分别表示出来 , 最后肯定是可以消掉A、B的 , 也就可以得到A+E+I的值 。
【宜宾学院|一道世界数学团体锦标赛真题,题目看似很难,其实很简单】这是一道世界数学团体锦标赛的真题 , 只看题目感觉挺难 , 但是下笔做过后 , 不少初中生都觉得很简单 。 你觉得难吗?
推荐阅读
- 中国科学院大学|我国进步最快的非211创办5年后成为双一流,分数线却直逼清华北大
- 江苏省|全国5所本科层次的警官学院介绍,被誉为“司法警官的摇篮”
- 高校|2020年高校更名之医学院校篇
- 数学|分享一道数学思考题,能做对者属于尖子生,难点是巧用面积公式
- 大学|补录是今年高考招生的最后一道“菜”,你知道吃上这菜有多难吗?
- 大学|这所学院改名为“大学”,名字很高大上,今年录取分数线暴涨!
- 抚州|江西这所大学即将脱离本部,失去211大学的头衔,降为二本学院
- 大学|教育部最新大学改名严令来了,独立学院更名不得包含原举办学校
- 湘南学院|二本考生注意:征集志愿来临,建议多了解这些大学,容易捡漏
- 大学|被理工学院录取,全家后悔不已:一年学费2万多,却是个民办大学
















