江苏龙网

  1. 首页 > 人文 > >

「普朗克常数」为什么不存在比普朗克长度更短的距离？


「普朗克常数」为什么不存在比普朗克长度更短的距离？
文章图片
「普朗克常数」为什么不存在比普朗克长度更短的距离？
文章图片
「普朗克常数」为什么不存在比普朗克长度更短的距离？
文章图片
早在公元前4世纪 ， 德谟克利特就提出了原子论 。 那时起 ， 人们逐渐认识到物质都是由原子组成的 ， 它们是一个个独立的不可分割的“坚固实体” 。 到亚里士多德这里 ， 他将“原子”具体化 ， 提出了物质的四元素说 ， 这起了更多人去关注“原子究竟是什么”、“一个原子与另一个原子之间有区别吗”等问题 。
关于对原子的具体认识 ， 争议了两千多年后的19世纪 ， 道尔顿提出了现代原子说 ， 从化学反应中元素比例的角度来说明原子的不可分割性 。 到了19世纪末期 ， 在一系列阴极射线实验研究成果的基础上 ， 汤姆逊成功从原子中分离出了电子 ， 自此 ， 人类探索了两千多年的不可分割的“原子”们 ， 陆续被揭开面纱 。
今天 ， 物理学家认为电子、组成核子的各类夸克、介子等基本粒子 ， 确确实实是不可再分割的 ， 因为它们已经是物质最基本的组成结构了 。
20世纪末期 ， 在尝试结合量子力学与广义相对论的过程中 ， 物理学家逐渐产生了这样一个想法：既然物质的组成结构不具有连续性 ， 物质不是无限可分的 ， 那么与物质相对应的空间（时间）是否也是不可无限分割的？是否存在最短的空间距离？
这样的想法够大胆了 ， 因为空间在所有人大脑中最原始的印象 ， 都是虚无、广阔、平滑连续的 。 那这样的想法在物理上有意义吗？它与基本粒子的不可分割性有什么关系？下面以电子为例进行说明 。
电子在量子场论中被视为一个0体积的点粒子 ， 在超弦理论中被视为一根共振的一维弦 。 我们可以在这两个理论对电子“形状”的不同描述上 ， 找到突破口 。 原来 ， 量子场论之所以不能作为融合量子力学与广义相对论的终极理论的候选模型 ， 就是因为点粒子假设的引入 。 而当认为基本粒子如电子 ， 并不是0体积的点粒子 ， 而是自身会占据空间一定长度或体积的粒子 ， 则很多场论计算结果中的无穷大都会消失 。
在意识到电子并不是点粒子之后 ， 电子的不可分割性和空间的某种不可分割性 ， 就可以被我们结合在一起 。 电子的不可分割性 ， 在物理上意味着 ， 对电子所占据的这一部分空间以任意形式进行划分 ， 其中划分得到的任意一块空间都是不具有真实性的 。 因此可以认为 ， 如果空间是无限可分的 ， 那就意味着电子在空间中将会是无限可分的 。
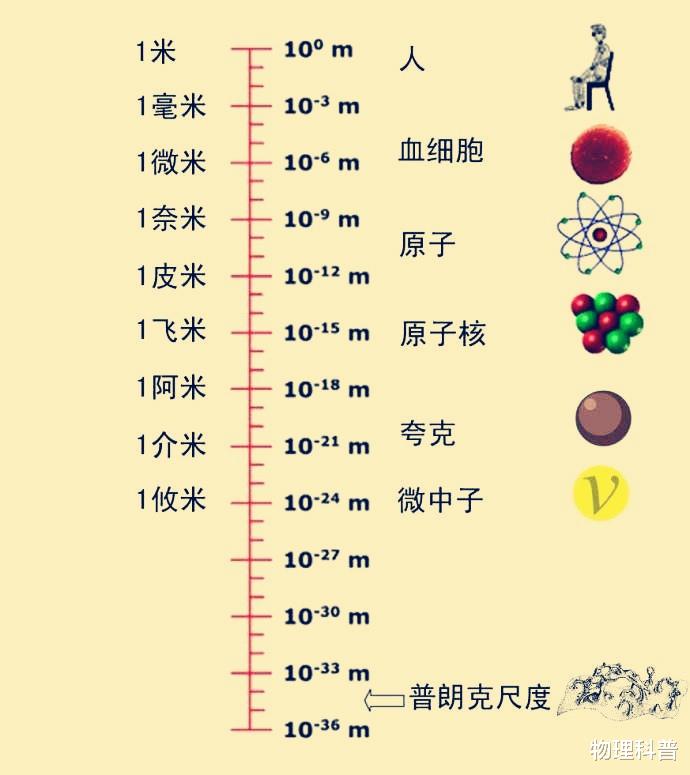
既然空间不是无限可分的 ， 那它就必定存在一个距离的下限 。 接下来我们需要找到这个空间距离 ， 它拥有现实空间中最短的长度 ， 任何比它“更短”的距离都没有物理意义 。 下面沿着物理学家的方法 ， 可以从一些与空间性质相关的基本常数出发 ， 去构造出最短的距离 。
符合条件的基本常数很显然是光速c、牛顿引力常数G、普朗克常数h 。 光速c是一切物质运动速度的上限 ， 因此它表示空间、时间某一方面的性质；根据广义相对论我们知道 ， 引力是可以在空间中被几何化的 ， 因此常数G表示空间、时间另一方面的性质；而现实空间的性质 ， 一定还与量子力学中最基本的普朗克常数有关 。 在这三个常数的组合之下 ， 通过适当的量纲运算 ， 就可以得到最短的距离——普朗克长度 。
那么为什么不存在比普朗克长度更短的距离？我们从上图可以清楚地看到 ， 在认定牛顿引力常数G和普朗克常数h都是不变量的基础上 ， 假如存在一个比普朗克长度更短的距离l ， 并且它是具有物理意义的 ， 那么距离l同样应该可以用G、h及速度v这三个参数表示出来 。 在这个表达式中 ， 与普朗克距离的表达式做对比 ， 就可以发现速度v已经大于光速了 。 而任何物质的速度都是不可能大于光速的 ， 因此上面的假设是不成立的 。


推荐阅读


上一篇：「」认识蚊子幼虫—孑孓

下一篇：「太阳系」去年地球要流浪，今年太阳系也要流浪，让我们一起丢掉三观